ассмотрим максимальное число победных игр: 75 : 3 = 25 (игр), но при таком варианте игр вничью быть не может.
Будем уменьшать число победных игр и считать, сколько за это команда получит очков. Предположим, что победных игр 24: 24 · 3 = 72. Таким образом, в данной конфигурации может быть 24 победы, 3 поражения и 3 ничьи.
Предположим, что победных игр 23: 23 · 3 = 69. Получаем, что 6 очков за ничью и 0 очков за поражение.
Предположим, что победных игр 22: 22 · 3 = 66. Получаем, что такой ситуации быть не может, так как максимальное число игр вничью — восемь, следовательно, 8 очков — 66 + 8 = 74, а в условии сказано, что команда набрала 75 очков.
Таким образом, наибольшее число ничейных матчей — 6.
Уравнением, равносильным заданному, может быть следующее:
34x - 46 = 23x + 24.
Объяснение:
Записать одно уравнение равносильное данному:
3,4x - 4,6 = 2,3x + 2,4.
Равносильными называются уравнения, множества корней которых совпадают. Если уравнения не имеют корней, то они тоже равносильны.1) Решим исходное уравнение, чтобы определить его корни.
3,4x - 4,6 = 2,3x + 2,4;
Перенесем неизвестные слагаемые в левую часть уравнения, а известные - в правую, сменив их знак на противоположный:
3,4x -2,3x = 2,4 + 4,6;
приведем подобные слагаемые:
1,1x = 7;
разделим обе части уравнения на коэффициент 1,1 и найдем корень уравнения:
Уравнение имеет один корень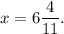
Воспользуемся свойствами равносильных преобразований уравнений.
2) Если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получится уравнение равносильное данному.
Перенесем неизвестные слагаемые в левую часть уравнения, а известные - в правую, сменив их знак на противоположный:
3,4x - 4,6 = 2,3x + 2,4;
3,4x -2,3x = 2,4 + 4,6;
1,1x = 7.
Получили уравнение равносильное данному, так как его корень равен корню заданного уравнения:
3) Если обе части уравнения разделить или умножить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.
Умножим обе части заданного уравнения на 10:
(3,4x - 4,6) · 10 = (2,3x + 2,4) · 10
34x - 46 = 23x + 24.
Найдем корни полученного уравнения.
34x - 23x = 46 + 24;
11x = 70;
Корень данного уравнения равен корню исходного уравнения. Получили уравнение, равносильное данному.
Запишем одно из полученных уравнений в ответ:
34x - 46 = 23x + 24.
ассмотрим максимальное число победных игр: 75 : 3 = 25 (игр), но при таком варианте игр вничью быть не может.
Будем уменьшать число победных игр и считать, сколько за это команда получит очков. Предположим, что победных игр 24: 24 · 3 = 72. Таким образом, в данной конфигурации может быть 24 победы, 3 поражения и 3 ничьи.
Предположим, что победных игр 23: 23 · 3 = 69. Получаем, что 6 очков за ничью и 0 очков за поражение.
Предположим, что победных игр 22: 22 · 3 = 66. Получаем, что такой ситуации быть не может, так как максимальное число игр вничью — восемь, следовательно, 8 очков — 66 + 8 = 74, а в условии сказано, что команда набрала 75 очков.
Таким образом, наибольшее число ничейных матчей — 6.
Пошаговое объяснение: