Математика: Решите систему уравнений методом гаусса:

Решите систему уравнений методом гаусса:

Показать ответ

Ответ:

vitek0000

17.02.2020 01:02

161) 38 см - периметр прямоугольника ABCD

162) 13,8 см длина прямоугольника

4,6 см ширина прямоугольника

Пошаговое объяснение:

№ 161.

Р ΔВМС = 36,6 см

36,6 : 3 = 12,2 (см) - длина каждой стороны ΔВМС : ВМ, МС и ВС, которая одновременно является длиной прямоугольника ABCD

Р ΔCND = 20,4 см

20,4 : 3 = 6,8 (см) - длина каждой стороны ΔCND: CN, ND и CD, которая одновременно является шириной прямоугольника ABCD

Р АВСD = 2(12,2 + 6,8) = 2 * 19 = 38 см - периметр прямоугольника ABCD

№ 162.

6,8 см - длина стороны квадрата

Р кв. = 4а = 4 *6,8 = 27,2 см - периметр квадрата

27,2 + 9,6 = 36,8 см - периметр прямоугольника

Р прям. = 2(а + b), где Р = 36,8 см, а - длина = 3х см, b - ширина = х см

2(3х + х) = 36,8

8х = 36,8

х = 36,8/8

х = 4,6 (см) ширина прямоугольника

3*4,6 = 13,8 (см) длина прямоугольника

0,0(0 оценок)

Ответ:

yxurcguh

16.07.2022 22:07

x∈ (-n-2;-n+2]

Пошаговое объяснение:

$a_n=\frac{1}{2^n}$

Вычислим радиус сходимости:

$R= \lim_{n \to \infty} \frac{a_n}{a_{n+1}}\\R= \lim_{n \to \infty} \frac{\frac{1}{2^n} }{\frac{1}{2^{n+1}} } = \lim_{n \to \infty} \frac{2*2^n}{2^n}=2$

Находим область сходимости степенного ряда:

$x_1=-n-2\\x_2=-n+2\\$

x∈(-n-2; -n+2)

Остаётся проверить сходимость ряда на концах данного интервала.

При х = -n-2 мы получим следующий ряд:

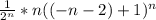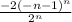
∑ $\frac{1}{2^n}*n((-n-2)+1)^n$ =∑ $\frac{-2(-n-1)^n}{2^n}$

Рассмотрим первых 3 члена данного ряда: -2; 1/8; -128

Данный ряд будем исследовать по признакам Лейбница

$\lim_{n \to \infty} \frac{2(-n-1)^n}{2^n} \\2\frac{1}{8}$

Как видим, выполняется лишь второе условие Лейбница, а значит ряд расходится => x=-n-2 является точкой расходимости.

Рассматриваем второй конец x=-n+2

Получаем следующий ряд

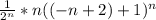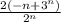
∑ $\frac{1}{2^n}*n((-n+2)+1)^n$ =∑ $\frac{2(-n+3^n)}{2^n}$

Тут исследуем по признакам Даламбера

$\lim_{n \to \infty} \frac{u_{n+1}}{u_n}=q$

q=1 - неопределённость, т.к. при q>1 ряд расходится, а при q<1 - сходится.

$\lim_{n \to \infty} \frac{\frac{2(-(n+1)+3)^{n+1}}{2^{n+1}} }{\frac{2(-n+3)^n}{2^n} }= \lim_{n \to \infty} \frac{2^{(-n+2)}^{n+1}}{2^{(-n+3)}^n} *\frac{2^n}{2^{n+1}}= \lim_{n \to \infty} \frac{2^{-n+2}^{n+1}}{2*2^{-n+3}^n} =\frac{1}{2}$