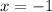При условии, что правая часть , возведем обе части уравнения в квадрат, получим
Произведение равно нулю, если хотя бы один из множителей равен нулю.
При этом нужно удостоверится, что эти корни будут принадлежать условию x≤0, то есть, нужно решить следующие неравенства:
- зависит от знаменателя, то есть откуда
также зависит от знаменателя, т.е. откуда
При уравнение имеет два корня
При уравнение имеет одно решение
При уравнение действительных корня не имеет
При уравнение имеет один корень
При условии, что правая часть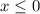
, возведем обе части уравнения в квадрат, получим
Произведение равно нулю, если хотя бы один из множителей равен нулю.
При этом нужно удостоверится, что эти корни будут принадлежать условию x≤0, то есть, нужно решить следующие неравенства:
При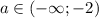
уравнение имеет два корня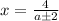 
При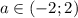
уравнение имеет одно решение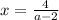 
При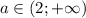
уравнение действительных корня не имеет
При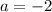
уравнение имеет один корень 