Из вершины В опускаем высоту ВN и получаем два прямоугольных треугольника АВN и СBN с общей стороной ВN. СN берем за Х и тогда АN=5+X По теореме Пифагора выводим BN^2 для двух треугольников: 1) ВN^2=АВ^2-АN^2=9^2-(5+X)^2=81-25-10X-X^2=56-10X-X^2 2) BN^2=BC^2-CN^2=36-X^2 Долее их уравниваем 56-10X-X^2=36-X^2 -10X-X^2+X^2=36-56 -10X=-20 X=2 Подставляем и находим ВN BN^2=36-2^2=32 BN=V32 Теперь из вершины В чертим отрезок ВL перпендикулярно плоскости М, это и есть расстояние между плоскостью М и вершиной В. Рассмотрит треугольник BNL, он прямоугольный и равнобедренный т.к. ВL перпендикулярно NL и угол ВNL равен 45 по условию. Опять же по теореме Пифагора выводим ВN^2 BN^2=BL^2+NL^2 так как ВN=V32 и ВL=NL то V32^2=2BL^2 32=2BL^2 BL^2=32/2 BL=V16 BL=4 ответ: расстояние между плоскостью М и вершиной В равно 4
Пошаговое объяснение:
169. Периметр параллелепипеда сумма всех его сторон. в основании квадрат, ⇒ а = б
а-длина
б-ширина = а
с- высота = а + 3 составляем уравнение
Р = 4*( а + б + с ) = 4 * (2а + с ) = 4 *(2а + а+3) = 4(3а+3)
12( а + 1 ) =60
а + 1 = 60 : 12
а + 1 = 5
а = 4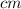
а=б=4 
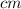с=7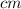 
Проверка Р = 4 ( 4 + 4 + 7 ) = 4 * 15 =60 см сошлось.
Sбок= Роснов* высоту= 4*4*7=112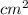
Sполн = Sбок+2Sосн = 112 + 2*4*4=112+32=144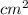
168 Sбок. = Росн.* h
обозначим за "х" - длина основания,
"у" - ширина основания Росн. = 2*( х + у )
составляющие Sбок.= 2(х + у) *h ; 2(х + у)*2=48
боковая поверхность складывается из двух пар прямоугольников:
составляем уравнение ( систему уравнений )
Sосн = 2* х * у = 2 * 5 * 7 = 70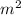
потому что их два, ( верхнее и нижнее)
проверка
Sбок. = 2*(5 + 7) * 2 = 2 * 12 * 2 = 48 сошлось
По теореме Пифагора выводим BN^2 для двух треугольников:
1) ВN^2=АВ^2-АN^2=9^2-(5+X)^2=81-25-10X-X^2=56-10X-X^2
2) BN^2=BC^2-CN^2=36-X^2
Долее их уравниваем
56-10X-X^2=36-X^2
-10X-X^2+X^2=36-56
-10X=-20
X=2
Подставляем и находим ВN
BN^2=36-2^2=32
BN=V32
Теперь из вершины В чертим отрезок ВL перпендикулярно плоскости М, это и есть расстояние между плоскостью М и вершиной В.
Рассмотрит треугольник BNL, он прямоугольный и равнобедренный т.к. ВL перпендикулярно NL и угол ВNL равен 45 по условию. Опять же по теореме Пифагора выводим ВN^2
BN^2=BL^2+NL^2 так как ВN=V32 и ВL=NL то
V32^2=2BL^2
32=2BL^2
BL^2=32/2
BL=V16
BL=4
ответ: расстояние между плоскостью М и вершиной В равно 4