Решите уравнения
1) ax-2x=a²-4;
2) cx-dx=5c-5d;
3) cbx-abx=b²c-ab²;
4) ax-bx=a²-b²

Показать ответ

Ответ:

sea131281

02.01.2020 05:32

(x^2 +2y)(x^2+2y)-(x^2-2y)(x^2 +2y)=

=(x^2 +2y)(x^2+2y-x^2+2y) =

=(x^2 +2y)*4y=4y(x^2 +2y)

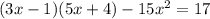
a) $(3x-1)(5x+4)-15x^{2} =17$

$15x^2-5x+12x-4-15x^{2} =17$

7x=17+4

7x=21

x=21:7

x=3

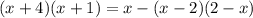
b) (x+4)(x+1)=x-(x-2)(2-x)

$x^{2} +4x+x+4=x+(x-2)(x-2)$

$x^{2} +5x+4=x+x^{2} -4$

4x=-8

x=-8:4

x=-2

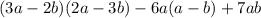3. (3a-2b)(2a-3b)-6a(a-b)+7ab =

=6a^2-4ab-9ab+6b^2-6a^2+6ab+7ab = 6b^2

Чтобы найти значение выражения, надо знать

только значение переменной b.

ответ: 3) Только переменной b.

Пусть х - цифра десятков, тогда

(12-х) - цифра единиц

получаем

10х+(12-х)= (9х+12) - данное двузначное число.

(12-х)*10+х= (120-9х) - обратное число к данному.

По условию: если к данному двузначному числу прибавить 54, то получится число, обратное данному.

Уравнение:

(9х+12) + 54 = (120-9х)

9х+9х = 120 -12-54

18х = 54

х = 54 : 18

х = 3 цифра десятков, тогда

12 - 3 = 9 - цифра единиц.

39 - данное двузначное число.

ответ: 39.

0,0(0 оценок)

Ответ:

timur123123

20.06.2022 22:52

Пусть А - выбраная случайно деталь - с номинальными размерами. За условием задачи, р = Р (А) =0,7, кю (английская буква) = 1 - 0,7 = 0,3. н=300, м1 =200, м2 = 250
Для вычисления этой вероятности используем функцию Лапласа: Р=Ф (х2) - Ф (х1)
Сначала найдем корень из произведения н*р*кю: корень из (н*р*кю) = корень из (300*0,7*0,3)корень из 63 = 7,94
х1=(200-300*0,7) / 7,94= - 1,26
х2=(250-300*0,7) / 7,94=5,04
С специальной таблицей находим значения функции Лапласа ля полученых значений х: Ф (5,04)=0,5; Ф (-1,26) = - Ф (1,26) = - 0,39617
Р=Ф (х2) - Ф (х1) = 0,5 - (- 0,39617) = 0,89617

0,0(0 оценок)

Популярные вопросы: Математика