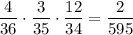Математика: Решите всё с пояснением и решениями

Общее число возможных элементарных исходов равно числу которыми можно извлечь 3 карты из 36:Подсчитаем число исходов, благоприятствующих данному событию:Два туза выбираем а один валет Итого — вероятность вытащить 2 туза и валет.ВТОРОЙ Первый туз можно достать с вероятностью , второй туз - а третий валет, с вероятностью , поскольку таких вариантов будет 12, {B1, T1, T2}, {B2,T1,T2}, {B3, T1,T2}, {B4,T1,T2}, {B1, T2, T3}, {B2,T2,T3}, {B3, T2,T3}, {B4,T2,T3}, {B1, T3, T4}, {B2,T3,T4}, {B3, T3,T4},...

Решите всё с пояснением и решениями

Показать ответ

Ответ:

jsowiwbdjwi

27.09.2020 12:43

20 задач

Пошаговое объяснение:

Количество задач, решенных в 1-й день:

(200·14%)/100%=2·14=28 задач.

x - количество задач, решенных в 3-й день.

x/1,5 - количество задач, решенных в 2-й день.

Количество задач, решенных в 5-й день:

3/2 ·x=1,5x

Количество задач, решенных в 4-й день:

5/8 ·x/1,5=5/8 ·(2x)/3=(5x)/12

Составляем уравнение:

28 +x/1,5 +x +(5x)/12 +1,5x=200

(2x)/3 +(5x)/2 +(5x)/12=200-28

8x+30x+5x=172·12

43x=172·12

x=(172·12)/43=4·12=48 задач, решенных в 3-й день.

Количество задач, решенных в 4-й день:

(5·48)/12=5·4=20 задач

0,0(0 оценок)

Ответ:

anutik4

05.11.2020 16:29

Общее число возможных элементарных исходов равно числу которыми можно извлечь 3 карты из 36:

$C^3_{36}=\dfrac{36!}{3!33!}=7140$

Подсчитаем число исходов, благоприятствующих данному событию:

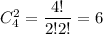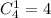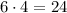
Два туза выбираем $C^2_4=\dfrac{4!}{2!2!}=6$ а один валет C^1_4=4 Итого $6\cdot 4=24$

$P=\dfrac{24}{7140}=\dfrac{2}{595}$ — вероятность вытащить 2 туза и валет.

ВТОРОЙ

Первый туз можно достать с вероятностью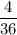 $\dfrac{4}{36}$ , второй туз - 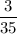$\dfrac{3}{35}$ а третий валет, с вероятностью 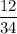$\dfrac{12}{34}$ , поскольку таких вариантов будет 12, {B1, T1, T2}, {B2,T1,T2}, {B3, T1,T2}, {B4,T1,T2}, {B1, T2, T3}, {B2,T2,T3}, {B3, T2,T3}, {B4,T2,T3}, {B1, T3, T4}, {B2,T3,T4}, {B3, T3,T4}, {B4,T3,T4}.