Род, число, падеж, склонение. Укажи время, лицо, число глаголов. У имен существительных
Ед...шь на кон..., отдыха...т под дерев. м, шага...шь по
дорог... пиш...т письмо, смотр...т телевизор, работа...т
в огород..., леж...т на стол..., поднима...т кран...м.
1)cos240 = cos(180 + 60)=cos (pi+pi/3)= -0.5, т.к. в 3 четверти косинус отрицателен
sin(2pi/3)=sin(120)=sin(180-60)=sin60=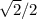
tg (-5pi/3)=-tg(300)=-tg(360-60)=-tg(-60)=tg60=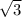
2)
a. 1-ctga*cosa*sina
1-(cos(a)/sin(a))*cos(a)*sin(a)= 1-cos²a= sin²a
б. sin (2pi+a)-cos(pi/2+a)=sina-(-sina)=2sina
4)sina/(1-cosa) + sina/(1+cosa)=(sin(1+cosa)+sina(1-cosa))/(1-cos^a)=2sina/sin^2a=2/sina
5)
cos^2 (a) * 1/ cos^2 (a) - sin^2 (a) = cos ^2 (a)
1-sin^2 (a) = cos^2 (a)
cos^2 (a) + sin^2 (a) = 1
чтд .
3) sin^2 (a) = 1 - cos^2 (a)
sin a=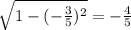
tg=sin/cos
tga=
ctg=cos/sin
ctga=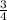
1.Из точки(A),не принадлежащей данной плоскости,проведены к ней две наклонные(AC&AD),сумма длин которых равна 28 см.Проекции этих наклонных на плоскость равны 6(BD) см и 8(BC) см.Найдите длины наклонных.
AB-перпендикуляр к плоскости
получили пирамиду.
составляем систему:
AC^2=AB^2+BC^2
AD^2=AB^2+BD^2
AD=28-AC,тогда:
AC^2=AB^2+BC^2
(28-AC)^2=AB^2+BD^2
AC^2=AB^2+BC^2
28^2-56AC+AB^2+BC^2=AB^2+BD^2
56AC=28^2+BC^2-BD^2
AC=(784+ 64-36)/56=14.5
AD=28-AC=28-14.5=13.5
2. Обозначим эту точку А, Первая наклонная АВ=10дм, вторая АС=18дм. Теперь проведем из точки А перпендикуляр на плоскость АН. Точки Н, В, С лежат на одной прямой, проведем эту прямую. НВ - первая проекция, НС - вторая. Получили два прямоугольные треугольника АНВ и АНС с общим катетом АН.
Пусть НВ=х, тогда НС=16-х.
Так как катет АН общий, то выразим этот катет из двух треугольников и приравняем.
АН^2=100-x, AH^2=324-(16-x)^2
100-x=324-(16-x)^2
100-x=324-256+32x-x^2
32x=32
x=1, HB=1см, тогда НС=16-1=15дм.
ответ: 1дм, 15дм.
Пошаговое объяснение:
3.