Теперь домножим первое равенство на 2, а второе - на 3:
Собака Лиса
Расстояние: 12 пр. = 22 пр.
Время: 12 пр. = 21 пр.
Итак, мы получили, что 12 прыжков собаки в точности равны 22 прыжкам лисы. Но проблема в том, что за то время, как собака делает те самые 12 прыжков, леса делает чуть меньше - 21 прыжок (а не 22). И, поэтому, скорость собаки () больше, чем скорость лисы():
Высота СD прямоугольного треугольника АВС, проведенная из вершины прямого угла, делит гипотенузу на отрезки АD и DB. Найдите катет АС, если DB=3,2 см, AD=1,8 см
Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
Проекция АС=АD=1,8, гипотенуза АВ=AD+DB=3,2+1,8=5 см
Тогда АС²=1,8*5=9⇒
АС=√9=3 см
–––––––––––––
2). Рисунок к первой задаче подходит и ко второй.
Высота CD прямоугольного треугольника АВС, проведенная из вершины прямого угла, делит гипотенузу АВ на отрезки АD и DB. Найдите гипотенузу АВ , если CD=6 см, а отрезок AD на 5 см короче отрезка DB.
Пусть DB=х.
Тогда AD=х-5
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Составим краткую запись к задаче:
Собака Лиса
Расстояние: 6 пр. = 11 пр.
Время: 4 пр. = 7 пр.
Теперь домножим первое равенство на 2, а второе - на 3:
Собака Лиса
Расстояние: 12 пр. = 22 пр.
Время: 12 пр. = 21 пр.
Итак, мы получили, что 12 прыжков собаки в точности равны 22 прыжкам лисы. Но проблема в том, что за то время, как собака делает те самые 12 прыжков, леса делает чуть меньше - 21 прыжок (а не 22). И, поэтому, скорость собаки (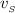
) больше, чем скорость лисы(
):
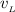1). Задача, данная в приложении:
Высота СD прямоугольного треугольника АВС, проведенная из вершины прямого угла, делит гипотенузу на отрезки АD и DB. Найдите катет АС, если DB=3,2 см, AD=1,8 см
Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
Проекция АС=АD=1,8, гипотенуза АВ=AD+DB=3,2+1,8=5 см
Тогда АС²=1,8*5=9⇒
АС=√9=3 см
–––––––––––––
2). Рисунок к первой задаче подходит и ко второй.
Высота CD прямоугольного треугольника АВС, проведенная из вершины прямого угла, делит гипотенузу АВ на отрезки АD и DB. Найдите гипотенузу АВ , если CD=6 см, а отрезок AD на 5 см короче отрезка DB.
Пусть DB=х.
Тогда AD=х-5
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
СD²=AD•B
36=х²-5х
х²-5х-36=0
Решив квадратное уравнение, получим
х₁=9
х₂= -4 ( не подходит)
ВD=9 см
AD=4 см
AB=9+4=13 см