По теореме Виета
x1+x2 = −p <=> -p = 5 < => p = -5
x1*x2 = q <=> q = 6
, подставляем значения p и q, получим:
Δ =
S = {2; 3)
х₁ = 3; х₂ = 2
Пошаговое объяснение:
х+у = 5
х•у = 6 → у = 6/х → подставим это значение у в первое уравнение:
х + 6/х = 5
х² + 6 = 5х
х² - 5х + 6 = 0 → Т.к. |a|=1, то можно воспользоваться теоремой Виета:
х² + pх + q = 0
↓
x₁ + x₂ = −p = 5
x₁ * x₂ = q = 6
x₁ + x₂ = 5 → x₁ = 3
x₁ * x₂ = 6 → х₂ = 2
По теореме Виета
x1+x2 = −p <=> -p = 5 < => p = -5
x1*x2 = q <=> q = 6
Δ =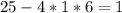
S = {2; 3)
х₁ = 3; х₂ = 2
Пошаговое объяснение:
х+у = 5
х•у = 6 → у = 6/х → подставим это значение у в первое уравнение:
х + 6/х = 5
х² + 6 = 5х
х² - 5х + 6 = 0 → Т.к. |a|=1, то можно воспользоваться теоремой Виета:
х² + pх + q = 0
↓
x₁ + x₂ = −p = 5
x₁ * x₂ = q = 6
x₁ + x₂ = 5 → x₁ = 3
x₁ * x₂ = 6 → х₂ = 2