Пошаговое объяснение:
Воспользуемся формулой понижения степени
Тогда
На единичной окружности отмечаем вертикальную линию соответствующую решению уравнения По условию задачи решением неравенства будут все точки окружности, лежащие левее прямой (см. рис.).
Пошаговое объяснение:
Воспользуемся формулой понижения степени
Тогда
На единичной окружности отмечаем вертикальную линию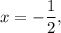 соответствующую решению уравнения
соответствующую решению уравнения 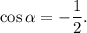 По условию задачи решением неравенства будут все точки окружности, лежащие левее прямой (см. рис.).
По условию задачи решением неравенства будут все точки окружности, лежащие левее прямой (см. рис.).