А) например, подойдет 8, уравнение 3t^2 - 8t + 4 = 0 Вообще, если неизвестный коэффициент обозначить за u, то подойдет любое u, для которого дискриминант u^2 - 4 * 3 * 4 = u^2 - 48 > 0
в) Нужно написать многочлен, корни которого t = -t1 и t = -t2. Это может быть, например, многочлен (t + t1)(t + t2) = (t + 2/3)(t + 2) Самый простой построить такой многочлен, не вычисляя корней, – воспользоваться теоремой Виета и её обратной. Для противоположных корней сумма меняет знак, а произведение остается прежним, так что 3t^2 + 8t + 4 подходит.
Поскольку многочлен, то у него есть значение в любой точке. (*)
Докажем утверждение по индукции.
База: - это то, что дано по условию.
Переход:
Пусть для некоторого верно; Докажем, что из этого следует справедливость утверждения и для ; Действительно, по предположению индукции множество решений уравнения совпадает с ; Возьмем от обеих частей (благодаря (*) мы можем это сделать): ; Но если сделать замену , получим ; А множество решений этого уравнения лежит в ; Предположим, что есть некоторый элемент , такой, что для него не найдется , чтобы ; Тогда , но лежит в , противоречие. Это завершает переход.
Вообще, если неизвестный коэффициент обозначить за u, то подойдет любое u, для которого дискриминант u^2 - 4 * 3 * 4 = u^2 - 48 > 0
б) D = 8^2 - 48 = 16 = 4^2
t = (8 +- 4)/6
t1 = (8 - 4)/6 = 2/3
t2 = (8 + 4)/6 = 2
в) Нужно написать многочлен, корни которого t = -t1 и t = -t2.
Это может быть, например, многочлен (t + t1)(t + t2) = (t + 2/3)(t + 2)
Самый простой построить такой многочлен, не вычисляя корней, – воспользоваться теоремой Виета и её обратной. Для противоположных корней сумма меняет знак, а произведение остается прежним, так что 3t^2 + 8t + 4 подходит.
Пусть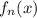 означает
означает 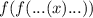 , где
, где 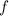 применена
применена 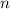 раз.
раз.
Поскольку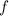 многочлен, то у него есть значение в любой точке. (*)
многочлен, то у него есть значение в любой точке. (*)
Докажем утверждение по индукции.
База: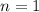 - это то, что дано по условию.
- это то, что дано по условию.
Переход:
Пусть для некоторого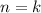 верно; Докажем, что из этого следует справедливость утверждения и для
верно; Докажем, что из этого следует справедливость утверждения и для 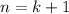 ; Действительно, по предположению индукции множество решений уравнения
; Действительно, по предположению индукции множество решений уравнения 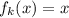 совпадает с
совпадает с 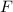 ; Возьмем
; Возьмем 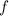 от обеих частей (благодаря (*) мы можем это сделать):
от обеих частей (благодаря (*) мы можем это сделать): 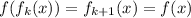 ; Но если сделать замену
; Но если сделать замену 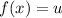 , получим
, получим 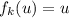 ; А множество решений этого уравнения лежит в
; А множество решений этого уравнения лежит в 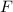 ; Предположим, что есть некоторый элемент
; Предположим, что есть некоторый элемент 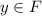 , такой, что для него не найдется
, такой, что для него не найдется  , чтобы
, чтобы 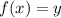 ; Тогда
; Тогда 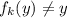 , но
, но 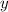 лежит в
лежит в 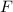 , противоречие. Это завершает переход.
, противоречие. Это завершает переход.