1) Переставим целые числа следующим образом: . Тогда мы можем поставить каждому из членов ряда одно из натуральных чисел: , а значит счетно.
2) Проведем через точку одну прямую. Тогда множество всех таких прямых задается углом между каждой из этих прямых и исходной прямой, лежащим в промежутке . Однако множество действительных чисел на отрезке несчетно, а значит и множество углов из промежутка несчетно, а тогда и множество прямых, задаваемых этими углами, несчетно.
3) Такое множество конечно.
4) Каждое четное положительное число имеет вид , а тогда можно поставить в соответствие каждому числу натуральное число , а тогда множество счетно.
Если мы округляем десятичные дроби до целых, правило такое: если цифра после запятой 5 или больше, то к числу целых прибавляем единицу, если меньше, то число целых не меняется
Пример: 0,6 + 0,7 = 1,3 ≈ 1
Но, если слагаемые округлить заранее (0,6 ≈ 1,0, и 0,7 ≈ 1) и сравнить с округлением суммы то:
(≈ 1 ) + (≈ 1) = (≈1)
Еще пример : 0,8 + 0,6 = 1,4
Есть еще один случай неправильного последовательного округления. Если задано округлить число сначала до сотых, потом до десятых, и в конце ло целых, то округлять надо исходное число, а не результат предыдущего округления
0,489 + 0, 478 = 0,967 ≈ 1,0
Но при неправильном округлении: 0,489 ≈ 0,490 ≈ 0,5 ≈ 1,0 , а 0,478 ≈0,480 ≈ 0,50 ≈ 1,0, Т.н опять можно получить 1 + 1 = 1
Все подобные казусы возникают при неправильных математических действиях
1) Переставим целые числа следующим образом: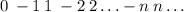
. Тогда мы можем поставить каждому из членов ряда одно из натуральных чисел: 
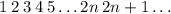, а значит 
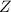счетно.
2) Проведем через точку одну прямую. Тогда множество всех таких прямых задается углом между каждой из этих прямых и исходной прямой, лежащим в промежутке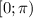
. Однако множество действительных чисел на отрезке ![[0;1]](/tpl/images/1041/0084/90495.png)
несчетно, а значит и множество углов из промежутка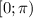 
несчетно, а тогда и множество прямых, задаваемых этими углами, несчетно.
3) Такое множество конечно.
4) Каждое четное положительное число имеет вид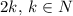
, а тогда можно поставить в соответствие каждому числу 
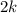натуральное число 
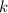, а тогда множество счетно.
5) Такое множество конечно.
Пошаговое объяснение:
Если мы округляем десятичные дроби до целых, правило такое: если цифра после запятой 5 или больше, то к числу целых прибавляем единицу, если меньше, то число целых не меняется
Пример: 0,6 + 0,7 = 1,3 ≈ 1
Но, если слагаемые округлить заранее (0,6 ≈ 1,0, и 0,7 ≈ 1) и сравнить с округлением суммы то:
(≈ 1 ) + (≈ 1) = (≈1)
Еще пример : 0,8 + 0,6 = 1,4
Есть еще один случай неправильного последовательного округления. Если задано округлить число сначала до сотых, потом до десятых, и в конце ло целых, то округлять надо исходное число, а не результат предыдущего округления
0,489 + 0, 478 = 0,967 ≈ 1,0
Но при неправильном округлении: 0,489 ≈ 0,490 ≈ 0,5 ≈ 1,0 , а 0,478 ≈0,480 ≈ 0,50 ≈ 1,0, Т.н опять можно получить 1 + 1 = 1
Все подобные казусы возникают при неправильных математических действиях