С 2 о SKM ty SKM SKM 604 SKM 604 50 50 40 1 40 30 30- 20 - 20- 10 у= 5 км/ч 10. ү= 15 км/ч 0 1 2 2 3 4 ч 0 1 2 3 4 tỷ 6) При системы координат удобно располагать два и более графика движения. Расположи график движения первого и второго лыжников на одном координатном углу в своей тетради. Подумай, сколько клеток нужно взять за единичный отрезок. ТВОРЧЕСКАЯ РАБОТА Составь свои вопросы к заданию 5. Задай их другу. 6
Прямая, которая задается уравнением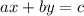 , можно переписать в виде функции
, можно переписать в виде функции 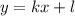 , где
, где 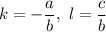
Коэффициент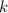 отвечает за наклон прямой, равный тангенсу угла
отвечает за наклон прямой, равный тангенсу угла 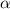 , образованного данной прямой и положительным направлением оси
, образованного данной прямой и положительным направлением оси 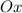 , то есть
, то есть 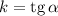
Если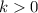 , то график функции возрастает.
, то график функции возрастает.
Если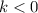 , то график функции убывает.
, то график функции убывает.
Если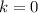 , то график ни возрастает, ни убывает — имеем прямую
, то график ни возрастает, ни убывает — имеем прямую 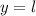 , параллельную оси абсцисс.
, параллельную оси абсцисс.
а) Пусть прямая проходит через две точки: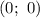 и
и 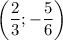
Тогда, подставляя соответствующие координаты точек в функцию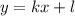 , получим систему двух линейных уравнений:
, получим систему двух линейных уравнений:
Тогда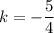 и
и 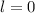
Так как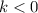 , то график функции убывает.
, то график функции убывает.
б) Пусть прямая проходит через две точки: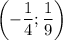 и
и 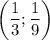 . Тогда
. Тогда
Тогда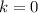 и
и 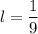
Так как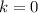 , то график функции ни возрастает, ни убывает.
, то график функции ни возрастает, ни убывает.
в) Пусть прямая проходит через две точки: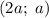 и
и 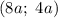 , где
, где 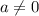 — параметр. Тогда
— параметр. Тогда
Умножим первое уравнение на 4 и получаем:
Тогда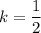 и
и 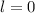
Так как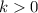 , то график функции возрастает.
, то график функции возрастает.
Посчитаем, сколько всего существует четырехзначных чисел.
Минимальное из них 1000, максимальное 9999.
9999 - 999 = 9000 чисел.
Найдем количество чисел, у которых в записи все цифры четные.
На первой позиции у них стоит цифра 2, 4, 6, 8 - 4 варианта выбора.
На второй, третьей и четвертой позициях - любая из 5 цифр: 0, 2, 4, 6, 8 - по 5 вариантов.
Всего комбинаций 4 * 5 * 5 * 5 = 20 * 25 = 500.
9000 - 500 = 8500 чисел.
ответ: Существует 8500 четырехзначных чисел, у которых хотя бы одна цифра в записи нечетная.
Пошаговое объяснение: