С—4. свойства функций
1. область определения функции, заданной графиком
на рисунке 13, — промежуток (-3; 4]. используя график,
перечислите свойства функции. найдите:
1) а) нули функции; б) промежут-
ки, в которых функция при -
нимает положительные значе
ния, и промежутки, в которых
функция принимает отрица
тельные значения;
2) промежутки, в которых функ:
ция возрастает и в которых
она убывает;
3) значение аргументах, при
котором функция принимает
наибольшее значение и при
котором она принимает наи
меньшее значение;
4) область значений функции.
рис. 13
Или в десятичной позиционной записи это выглядит так:
Найдём отношение abcde : bcde
Чтобы искомое число было наибольшим отношение
д.б. минимальным.
Пусть а = 9, т.е. взяли наибольшую цифру.
Теперь остаётся подобрать наименьшее t ≥ 1, чтобы выражение bcde имело цифры, не равные нулю. Такое число равно t = 16.
90000 : 16 = 5625
Получаем число 90000 + 5625 = 95625, у которого, отбросив старший разряд, получим делитель исходного числа, т.е. 95625 : 5625 = 17.
А теперь обращаем внимание. что число 5625 обладает теми же свойствами, что и полученное число, т.е.:
5625 : 625 = 9
625 : 25 = 25
25 : 5 = 5
Итак, число найдено, это
95625
1. 1 500 в отношении 1 к 3 - это 375 : 1 125
1) 1 + 3 = 4 (части) - всего
2) 1 500 : 4 = 375 - 1 часть
3) 375 · 3 = 1125 - 3 части
**************************************
2. 369 в отношении
к 
- это 246 : 123
1)
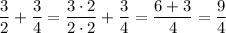(частей) - всего
2)
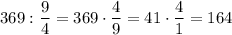- 1 часть
3)
- 
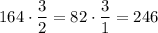части
4)
- 
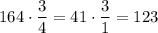части
****************************************
3. 1 т в отношении 5 к 3 - это 625 : 375 кг
1 т = 1 000 кг1) 5 + 3 = 8 (частей) - всего
2) 1 000 : 8 = 125 (кг) - 1 часть
3) 125 · 5 = 625 (кг) - 5 частей
4) 125 · 3 = 375 (кг) - 3 части
*****************************************
4. 12 км в отношении 16 к 14 - это 64 000 : 56 000 дм
1 км = 1 000 м1 м = 10 дм⇒ 1 км = 1 000 · 10 = 10 000 дм⇒ 12 км = 12 · 10 000 = 120 000 дм
1) 16 + 14 = 30 (частей) - всего
2) 120 000 : 30 = 4 000 (дм) - 1 часть
3) 4 000 · 16 = 64 000 (дм) - 16 частей
4) 4 000 · 14 = 56 000 (дм) - 14 частей