Число записать в числителе, а в знаменателе - единицу.
напр.:
16.
дробь, числитель и знаменатель которой равны, равна единице.
дробная черта - это знак деления; если число разделить на себя же, то получится 1:
18.
умножить целое на единицу части, затем умножить на кол-во частей:
найти от 28.
1) 28:7=4
2) 4*4=16.
умножить число на эту часть:
найти от 28.
19.
разделить часть (число) на кол-во единиц части в части (в числе), затем умножить на кол-во частей в целом:
найти целое, если от него
1)16:4=4
2)4*7=28.
разделить часть (число) на эту часть (дробь):
20.
Основное свойство дроби - если числитель и знаменатель умножить или разделить на одно и то же число, то новая дробь будет численно равна данной.
21.
Сокращение дроби - преобразование дроби, при котором числитель и знаменатель делят на такое число (НОД), после которого дробь становится несократимой (когда нет таких натуральных чисел, на которые можно было бы разделить числитель и знаменатель)
Но тем не менее, разложить на множители подкоренные выражения стоит :
x^2-5x-6 =(x-6)*(x+1) - теорема Виета
Снова по теореме Виета :
-x^2+18*x-72 = (x-6)*(12-x)
Для 3 радикала я очень хитро придумал : (для удобства преобразую для -)
- (x^3 -17*x^2 +89*x -138)
x^3 -17*x^2 +66*x +23*x -138 = x*(x^2-17*x +66) + 23*(x-6)
Именно такой трехчлен в скобках сделал неспроста:
x^2-17x +66 = (x-6)*(x-11) - по теореме Виета
x*(x-6)*(x-11) +23*(x-6) = (x-6)*(x^2-11x +23)
Теперь можно упростить вынеся √(x-6) за скобки :
(√(12-x) +√(-x^2+11*x-23) - √(x+1) ) *√(x-6) = 0
Стоит сразу отметить , что 6<=x <=12
Один корень уже известен :
x1=6
√(12-x) +√(-x^2+11*x-23) - √(x+1) = 0
x^2-11*x+23 = (12-x)*(x+1) -35
√(12-x) +√ ( (12-x)*(x+1) -35 ) - √(x+1) = 0
√(x+1) - √(12-x) = √ ( (12-x)*(x+1) -35 )
Возводим в квадрат :
x+1 -2*√( (x+1)*(12-x) ) +12-x = (12-x)*(x+1) -35
13- 2*√( (x+1)*(12-x) ) = (12-x)*(x+1) -35
Замена : √( (x+1)*(12-x) ) = t >=0
13 -2t =t^2 -35
t^2 +2t -48 = 0
По теореме Виета :
t1 = 6
t2 = -8 < 0 (не подходит)
√ ( (x+1)*(12-x) ) = 6
(x+1)*(12-x) = 36
x^2 -11*x +24=0
По теореме Виета :
x1=3 < 6 не подходит
x2=8 (предварительно подходит)
Поскольку ОДЗ мы не нашли , то для x=8 придется сделать проверку
√(12-x) +√ ( (12-x)*(x+1) -35 ) - √(x+1) = 0
√4 +√(36-35) -√9 = 2+1-3 = 0 - верно .
ответ : x1=6 ; x2=8
Число записать в числителе, а в знаменателе - единицу.
напр.: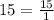
16.дробь, числитель и знаменатель которой равны, равна единице.
дробная черта - это знак деления; если число разделить на себя же, то получится 1: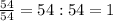
18.умножить целое на единицу части, затем умножить на кол-во частей:
найти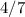
от 28.
1) 28:7=4
2) 4*4=16.
умножить число на эту часть:
найти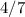
от 28.
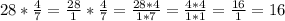
19.разделить часть (число) на кол-во единиц части в части (в числе), затем умножить на кол-во частей в целом:
найти целое, если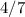
от него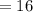 
1)16:4=4
2)4*7=28.
разделить часть (число) на эту часть (дробь):
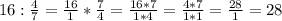
20.Основное свойство дроби - если числитель и знаменатель умножить или разделить на одно и то же число, то новая дробь будет численно равна данной.
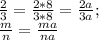
21.Сокращение дроби - преобразование дроби, при котором числитель и знаменатель делят на такое число (НОД), после которого дробь становится несократимой (когда нет таких натуральных чисел, на которые можно было бы разделить числитель и знаменатель)