С.
исследовать дифференциального исчисления функцию f(x)=x^2-9x^2+24x и построить её график.

300 см² и 200 см².

Пошаговое объяснение:

В прямом параллелепипеде боковое ребро равно 10 см, стороны основания 23 см и 11 см, диагонали основания относятся как 2: 3. Найти площади диагональных сечений.

Пусть дан прямой параллелепипед .

= 10 cм, АВ = 23см, ВС =11 см. Диагонали  BD : AC =2:3.

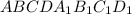Основанием прямой призмы является параллелограмм АВСD.

Найдем диагонали параллелограмма. По свойству квадратов диагоналей параллелограмма : сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

AC²+BD ² = 2· (AB² + BC²)

Пусть АС = 3х см, а ВD = 2х см. Тогда

(3x)² +(2x)² = 2· ( 23² +11²);

9x² +4x² =2 ·( 529 + 121);

13 x² = 2· 650;

13 x² = 1300;

x² = 1300 : 13;

x²= 100;

x= 10.

Тогда АС = 3· 10 = 30 см, ВD =2· 10 = 20 см.

Диагональное сечение - это прямоугольник, так как параллелепипед прямой.

Чтобы найти площадь прямоугольника надо длину умножить на ширину.

Прямоугольник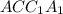 - диагональное сечение

см².

Прямоугольник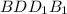 - диагональное сечение

см².

#SPJ1

Спростімо перший вираз:

6(4+a) - 8(a+5)

Почнемо з розподілення множників всередині дужок:

= 6 * 4 + 6 * a - 8 * a - 8 * 5

= 24 + 6a - 8a - 40

Згрупуємо подібні члени:

= (6a - 8a) + (24 - 40)

= -2a - 16

Таким чином, спрощений вираз 6(4+a) - 8(a+5) дорівнює -2a - 16.

Спростімо другий вираз:

-а - (-2а + 4б) + (7а - 3б)

Від'ємний знак перед дужкою -2а + 4б можна змінити на плюс, розподіливши його на всередині дужки:

= -а + 2а - 4б + 7а - 3б

= (-а + 2а + 7а) + (-4б - 3б)

= 10а - 7б

Таким чином, спрощений вираз -а - (-2а + 4б) + (7а - 3б) дорівнює 10а - 7б.