Здравствуй! Я с удовольствием помогу тебе разобраться с заданиями по теме "взаимно обратные функции"!
Задание 8:
В этом задании тебе нужно определить, являются ли данные функции взаимно обратными. Для этого необходимо проверить, выполняется ли условие обратности: если для любого значения x мы получаем y при применении функции f(x), и затем при подстановке этого y в функцию g(y) мы получаем исходное значение x, то функции f(x) и g(y) являются взаимно обратными.
Давай применим данное условие к первым двум функциям. Функция f(x) = -2x + 3 и функция g(y) = (3 - y) / 2.
1. Подставим значение x = 4 в функцию f(x): f(4) = -2 * 4 + 3 = -8 + 3 = -5.
2. Теперь подставим полученное значение y = -5 в функцию g(y): g(-5) = (3 - (-5)) / 2 = (3 + 5) / 2 = 8 / 2 = 4.
Мы получили исходное значение x = 4, поэтому эти две функции являются взаимно обратными.
Теперь проверим последние две функции. Функция f(x) = (x^2 - 2) / 3 и функция g(y) = sqrt(3y + 2).
1. Подставим значение x = 2 в функцию f(x): f(2) = (2^2 - 2) / 3 = (4 - 2) / 3 = 2 / 3.
2. Теперь подставим полученное значение y = 2/3 в функцию g(y): g(2/3) = sqrt(3 * (2/3) + 2) = sqrt(2 + 2) = sqrt(4) = 2.
Мы получили исходное значение x = 2, значит эти функции также являются взаимно обратными.
Таким образом, все четыре функции являются взаимно обратными.
Задание 9:
В этом задании тебе нужно найти значения функций f(x) и g(y) для заданных значений x и y, а также определить, являются ли эти значения парой взаимно обратных функций.
Значение функции f(x) = -3x + 5 при x = -2:
f(-2) = -3 * (-2) + 5 = 6 + 5 = 11.
Значение функции g(y) = (5 - y) / 3 при y = 11:
g(11) = (5 - 11) / 3 = (-6) / 3 = -2.
Мы получили значения f(x) = 11 и g(y) = -2. Они не являются парой взаимно обратных функций, так как при подстановке одного значения в функцию не получается исходное значение.
Задание 10:
В этом задании тебе нужно найти значение функции f(g(x)) и функции g(f(x)) для заданных функций f(x) и g(x).
Для начала, найдем значение функции f(g(x)):
f(g(x)) = f(4x - 1).
Подставим выражение g(x) = 4x - 1 в функцию f(x):
f(g(x)) = f(4x - 1) = -3(4x - 1) + 5 = -12x + 3 + 5 = -12x + 8.
Теперь найдем значение функции g(f(x)):
g(f(x)) = g(-3x + 5).
Подставим выражение f(x) = -3x + 5 в функцию g(x):
g(f(x)) = g(-3x + 5) = 5 - (-3x + 5) / 3 = 5 + (3x - 5) / 3 = (15 + 3x - 5) / 3 = (3x + 10) / 3 = x + 10/3.
Таким образом, значение функции f(g(x)) равно -12x + 8, а значение функции g(f(x)) равно x + 10/3.
Пошаговое объяснение:
функция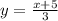
обратная ей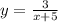 
функция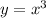
обратная ей ![y= \sqrt[3]{x}](/tpl/images/1686/6641/65493.png)
функция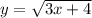
обратная ей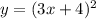 
Задание 8:
В этом задании тебе нужно определить, являются ли данные функции взаимно обратными. Для этого необходимо проверить, выполняется ли условие обратности: если для любого значения x мы получаем y при применении функции f(x), и затем при подстановке этого y в функцию g(y) мы получаем исходное значение x, то функции f(x) и g(y) являются взаимно обратными.
Давай применим данное условие к первым двум функциям. Функция f(x) = -2x + 3 и функция g(y) = (3 - y) / 2.
1. Подставим значение x = 4 в функцию f(x): f(4) = -2 * 4 + 3 = -8 + 3 = -5.
2. Теперь подставим полученное значение y = -5 в функцию g(y): g(-5) = (3 - (-5)) / 2 = (3 + 5) / 2 = 8 / 2 = 4.
Мы получили исходное значение x = 4, поэтому эти две функции являются взаимно обратными.
Теперь проверим последние две функции. Функция f(x) = (x^2 - 2) / 3 и функция g(y) = sqrt(3y + 2).
1. Подставим значение x = 2 в функцию f(x): f(2) = (2^2 - 2) / 3 = (4 - 2) / 3 = 2 / 3.
2. Теперь подставим полученное значение y = 2/3 в функцию g(y): g(2/3) = sqrt(3 * (2/3) + 2) = sqrt(2 + 2) = sqrt(4) = 2.
Мы получили исходное значение x = 2, значит эти функции также являются взаимно обратными.
Таким образом, все четыре функции являются взаимно обратными.
Задание 9:
В этом задании тебе нужно найти значения функций f(x) и g(y) для заданных значений x и y, а также определить, являются ли эти значения парой взаимно обратных функций.
Значение функции f(x) = -3x + 5 при x = -2:
f(-2) = -3 * (-2) + 5 = 6 + 5 = 11.
Значение функции g(y) = (5 - y) / 3 при y = 11:
g(11) = (5 - 11) / 3 = (-6) / 3 = -2.
Мы получили значения f(x) = 11 и g(y) = -2. Они не являются парой взаимно обратных функций, так как при подстановке одного значения в функцию не получается исходное значение.
Задание 10:
В этом задании тебе нужно найти значение функции f(g(x)) и функции g(f(x)) для заданных функций f(x) и g(x).
Для начала, найдем значение функции f(g(x)):
f(g(x)) = f(4x - 1).
Подставим выражение g(x) = 4x - 1 в функцию f(x):
f(g(x)) = f(4x - 1) = -3(4x - 1) + 5 = -12x + 3 + 5 = -12x + 8.
Теперь найдем значение функции g(f(x)):
g(f(x)) = g(-3x + 5).
Подставим выражение f(x) = -3x + 5 в функцию g(x):
g(f(x)) = g(-3x + 5) = 5 - (-3x + 5) / 3 = 5 + (3x - 5) / 3 = (15 + 3x - 5) / 3 = (3x + 10) / 3 = x + 10/3.
Таким образом, значение функции f(g(x)) равно -12x + 8, а значение функции g(f(x)) равно x + 10/3.