Заметим, что основание логарифма меньше единицы. Это означает, чтобы значение самого логарифма было больше ноля (как требуется в неравенстве), нужно, чтобы его подлогарифмическое выражение было тоже меньше единицы (и больше ноля, в силу области определения логарифмических выражений):
Все это можно довести до метода интервалов:
Первое неравенство можно решить так:
- - - + + +
____________________
Второе неравенство решается схожим образом:
- - - + + + - - -
___________________________ Или , или .
Как пересечение решений двух неравенств имеем решение .
Значит, наименьшее целое число, удовлетворяющее неравенству - это , что сходится с ответом.
Заметим, что основание логарифма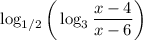 меньше единицы. Это означает, чтобы значение самого логарифма было больше ноля (как требуется в неравенстве), нужно, чтобы его подлогарифмическое выражение было тоже меньше единицы (и больше ноля, в силу области определения логарифмических выражений):
меньше единицы. Это означает, чтобы значение самого логарифма было больше ноля (как требуется в неравенстве), нужно, чтобы его подлогарифмическое выражение было тоже меньше единицы (и больше ноля, в силу области определения логарифмических выражений):
Все это можно довести до метода интервалов:
Первое неравенство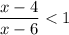 можно решить так:
можно решить так:
- - - + + +
__________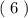 __________
__________ 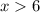
Второе неравенство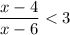 решается схожим образом:
решается схожим образом:
- - - + + + - - -
_________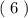 _________
_________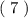 _________ Или
_________ Или 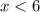 , или
, или 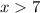 .
.
Как пересечение решений двух неравенств имеем решение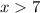 .
.
Значит, наименьшее целое число, удовлетворяющее неравенству - это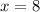 , что сходится с ответом.
, что сходится с ответом.
ответ: 8.