Мы знаем, что скорость первого мотоциклиста была 72 км/ч. Он проехал 25 мин. Мы можем узнать, какое расстояние он преодолел за 25 минут. НО скорость нам дана в км/ч, а время в минутах, поэтому нельзя умножать 72 на 25, потому что совершенно разные единицы измерения, значит необходимо перевести минуты в часы:
25мин=ч
Находим расстояние, которое проехал первый мотоциклист за 25 минут или за 5/12 часа:
км
Пусть скорость второго мотоциклиста будет равна х, тогда найдем какое расстояние преодолел второй мотоциклист за 5/12 часа;
*xкм проехал второй мотоциклист за 25 минут.
По условию известно, что между ними было расстояние 2 км, а первый мотоциклист проехал 30км,это значит, что второй мотоциклист проехал 30-2=28км за 25 минут.
Составим уравнение и найдем скорость второго мотоциклиста:
Проведем на сторону АD высоту ОК, которая будет и медианой и биссектрисой, так как треугольник АОD равнобедренный. Треугольник ОКD - прямоугольный. Выходя из того, что ОК - биссектриса, угол КОD = угол АОD/2 = 120/2 = 60 градусов. Гипотенуза ОD = ВD/2 = 12/2.
sin KOD = KD/OD , отсюда КD = ОD*sin KOD = 6*sin 60 = 6*√3/2 = 3√3.
Так как АК = КD, то АD = АК + КD = 3√3 + 3√3 = 6√3 .
67,2 км/ч
Пошаговое объяснение:
Мы знаем, что скорость первого мотоциклиста была 72 км/ч. Он проехал 25 мин. Мы можем узнать, какое расстояние он преодолел за 25 минут. НО скорость нам дана в км/ч, а время в минутах, поэтому нельзя умножать 72 на 25, потому что совершенно разные единицы измерения, значит необходимо перевести минуты в часы:
25мин=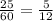 ч
ч
Находим расстояние, которое проехал первый мотоциклист за 25 минут или за 5/12 часа:
Пусть скорость второго мотоциклиста будет равна х, тогда найдем какое расстояние преодолел второй мотоциклист за 5/12 часа;
По условию известно, что между ними было расстояние 2 км, а первый мотоциклист проехал 30км,это значит, что второй мотоциклист проехал 30-2=28км за 25 минут.
Составим уравнение и найдем скорость второго мотоциклиста:
Удачи!
Дано прямоугольник ABCD, O - точка пересечения диагоналей прямоугольника, угол СOD = 60 градусов, АС = ВD = 12.
Так как угол СOD = углу ВОА = 60 градусов, то угол ВСО = углу АОD = (360 - (60 + 60))/2 = (360 - 120)/2 = 240/2 = 120 градусов.
Проведем на сторону АD высоту ОК, которая будет и медианой и биссектрисой, так как треугольник АОD равнобедренный. Треугольник ОКD - прямоугольный. Выходя из того, что ОК - биссектриса, угол КОD = угол АОD/2 = 120/2 = 60 градусов. Гипотенуза ОD = ВD/2 = 12/2.
sin KOD = KD/OD , отсюда КD = ОD*sin KOD = 6*sin 60 = 6*√3/2 = 3√3.
Так как АК = КD, то АD = АК + КD = 3√3 + 3√3 = 6√3 .