с условием и решением задачи.Подписка лайк и ЛуЧший ответ
​

надо работать по действиям. Умножаем-3 1/8 на числа из первой скобки, а 7 1/2 на числа из второй скобки. раскроем скобки.

1)-3 1/8×4/5х=-25/8×4/5х=-5/2×1/1х=-5/2х

2) -3 1/8×3/25у=-25/8×3/25у=-5/8×3/5у=-15/40у

3) -3 1/8×(-8z)=-25/8×(-8/1z)=-25/1×(-1/1)z=25/1z=25z

раскрыв первую скобку получилось

-5/2х+(-15/40у)+25z

Теперь раскрываем вторую скобку

4) 7 1/2×2/3х=15/2×2/3х=5/1×1/1х=5/1х=5x

5) 7 1/2×9/15у=15/2×9/15у=1/2×9/1у=9/2у

6) 7 1/2×(-10)z=15/2×(-10/1)z=15/1×(-5/1)z=-75/1z=-75z

получаем

5х+9/2у-75z

теперь соединяем

-5/2х-15/40у+25z+5x+9/2y-75z=-5/2x+5x-15/40y+9/2y+25z-75z=

и соединяем х с х, у и у , z и z

=5/2x+33/8y-50z -это ответ

Пошаговое объяснение:

если где-то ошибалась, извени я просто объяснила суть

Площадь фигуры, ограниченной данными линиями

  ед.²

Пошаговое объяснение:

Надо вычислить площадь фигуры, ограниченной линиями:

1. Для того, чтобы вычислить площадь фигуры, надо построить эти графики и найти точки их пересечения:

Первый график - парабола, ветви вверх.

Второй график - это ось 0х.

Если у = 0, то

Формулы для вычисления площади фигуры, ограниченной линиями:

также нам понадобится формула Ньютона - Лейбница:

2. В нашем случае:

f₂(x) = 0 (ограничивает сверху);   f₁(х) = х² - 4х (ограничивает снизу);

b = 0;   a = 4.

Подставим эти значения в формулу (1) и с формулы (2) вычислим площадь фигуры:

 (ед²)

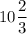⇒ площадь искомой фигуры    ед.²