с заданиями по Дискретной математике. Если возможно, то с подробным решением

Показать ответ

Ответ:

fjjjfg

04.11.2022 17:42

Произведение - это умножение ( * )
частное - деление ( :)
Сумма - сложение (+)

1. Пусть неизвестное число - а, произведение неизвестного числа (а) и числа 16, то есть: а * 16
сумма чисел 2136 и 1000 - это: 2136 + 1000
"Произведение неизвестного числа и числа 16 равно сумме чисел 2136 и 1000", значит: а * 16 = 2136 + 1000 - дальше решаем уравнение,
   а * 16 = 3136
  а = 3136/16
а = 196
Так как мы взяли а за неизвестное число, то значение а соответствует значению неизвестного числа, проще говоря: неизвестное число - 196.
Можно сделать проверку, вместо слова неизвестное число подставить 196 и посчитать, если левая и правая части примера окажутся равными, то всё решено верно:
196 * 16 = 2136 + 1000
3136 = 3136 - решено верно

неизвестное число - 196

2. Пусть неизвестное число - х, тогда ("частное числа 55350 и неизвестного числа"): 55350 : х
"произведение чисел 15 и 5" значит: 15 * 5
Теперь собирём всё вместе: "частное числа 55350 и неизвестного числа равно произведение чисел 15 и 5": 55350 : х = 15 * 5
55350 : х = 75
х = 55350/75
х = 738

Проверка: 55350 : 738 = 15 * 5
75 = 75 - всё верно, значит

неизвестное число - 738

0,0(0 оценок)

Ответ:

raku13

07.09.2020 09:23

ответ: $\begin{array}{|c|c|c|c|c|}R & r & a_n & P & S\\3\sqrt{2} & 3 & 6 & 24 & 36\\2\sqrt{2} & 2 & 4 & 16 & 16\\4 & 2\sqrt{2} & 4\sqrt{2} & 16\sqrt{2} & 32\\7\sqrt{2} & 3,5 & 7 & 28 & 49\\2\sqrt{2} & 2 & 4 & 16 & 16\\\end{array}$

Пошаговое объяснение:

Заданы формулы для правильного многоугольника.

В нашем случае правильного четырехугольника или квадрата.

Заданы формулы:

Длина многоугольника через радиус описанной окружности

$a_n=2R \cdot sin\frac{180^o}{n}$

Для квадрата

$a_4=2R \cdot sin\frac{180^o}{4}=2R \cdot sin(45^o)=2R\cdot\frac{\sqrt{2}}{2}=\sqrt{2}R$

или

$R=\frac{\sqrt{2}}{2}a_4$

Радиус вписанной окружности через радиус описанной окружности

$r=Rcos(\frac{180^o}{n})$

Для квадрата

$r=Rcos(\frac{180^o}{4})=Rcos(45^o)=\frac{\sqrt{2}}{2}R$

или

$R=\sqrt{2}r$

Площадь многоугольника через периметр и радиус вписанной окружности

$S=P\cdot r/2$ или S =a_4^2

Определим значения первой строки таблицы зная, что сторона квадрата a = 6.

Радиус описанной окружности

$R=\frac{\sqrt{2}}{2}\cdot 6=3\sqrt{2}$

Радиус вписанной окружности

$r=\frac{\sqrt{2}}{2}\cdot3\sqrt{2}=3$

Периметр

$P= 4a_4=4\cdot6=24$

Площадь квадрата

$S=24\cdot 3/2 = 36$

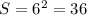
или S= 6^2=36

Определим значения второй строки таблицы зная, что радиус вписанной окружности r=2.

Радиус описанной окружности

$R=2\sqrt{2}$

Длина стороны квадрата

$a_4=\sqrt{2}\cdot2\sqrt{2}=4$

или

$a_4=2r=2\cdot2=4$

Периметр

$P= 4a_4=4\cdot4=16$

Площадь квадрата

$S=16\cdot 2/2 = 16$

Определим значения третьей строки таблицы зная, что радиус описанyой окружности R=4.

Длина стороны квадрата

$a_4=4\sqrt{2}$

Радиус вписанной окружности

$r=\frac{\sqrt{2}}{2}\cdot4=2\sqrt{2}$

Периметр

$P= 4a_4=4\cdot4\sqrt{2}=16\sqrt{2}$

Площадь квадрата

$S=16\sqrt{2}\cdot 2\sqrt{2}/2 = 32$

Определим значения четвертой строки таблицы зная, что периметр квадрата P=28.

Длина стороны квадрата

a_4=P/4 =28/4=7

Радиус описанной окружности

$R=\frac{\sqrt{2}}{2}\cdot 7$

Радиус вписанной окружности

$r=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{2}}{2}\cdot 7=3,5$

Площадь квадрата

$S=28\cdot \frac{3,5}{2} = 49$

Определим значения пятой строки таблицы зная, что площадь квадрата S=16.

Длина стороны квадрата

$a_4=\sqrt(S) =\sqrt(16)=4$

Далее как для второй строки.

Повторять не буду

Подставим значения в таблицу

$\begin{array}{|c|c|c|c|c|}R & r & a_n & P & S\\3\sqrt{2} & 3 & 6 & 24 & 36\\2\sqrt{2} & 2 & 4 & 16 & 16\\4 & 2\sqrt{2} & 4\sqrt{2} & 16\sqrt{2} & 32\\7\sqrt{2} & 3,5 & 7 & 28 & 49\\2\sqrt{2} & 2 & 4 & 16 & 16\\\end{array}$

0,0(0 оценок)

Популярные вопросы: Математика