С6 дана бесконечная арифметическая прогрессия, первый член которой равен 1998 а разность 13. каждый член прогрессии заминили суммой его цифр.получилось последовательность однозначных чисел. а)найти 300член получившийся прогрессии, б)сумму первых трехсот членов получившийся прогрессии, в) чуму ровна наименьщая сумма 350 членов этой прогрессии

Показать ответ

Ответ:

ba150704

17.06.2020 05:13

дана бесконечная арифметическая прогрессия, первый член которой равен 1998 а разность 13. каждый член прогрессии заминили суммой его цифр.С полученой последовательностью поступили так же и действовали до тех пор, пока не получилось последовательность однозначных чисел.

а) Халявный : трехсотый член член исходной прогрессии равен 1998+13*299=5885

5+8+8+5=26

2+6=8

б) Утверждение. Сумма цифр числа дает такой же остаток от деления на 9, что и само число.

Доказательство. Рассмотрим число

$a_n\cdot10^n+a_{n-1}\cdot10^{n-1}+\dots+a_1\cdot10+a_0$

(число, в десятичной записи составленное из цифр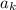 a_k ).

Из разложения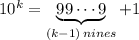 $10^k=\underbrace{99\cdots9}_{(k-1)\,nines}+1$ следует требуемое утверждение.

Следствие. Последовательность, получившаяся в задании, состоит из остатков от деления на 9 членов исходной прогрессии, в которой все нули заменены девятками.

1998 mod 9 = 0, поэтому первый член прогрессии - 9.

13 mod 9 = 4, поэтому второй член прогрессии 0+4=4, третий 4+4=8, четвертый (8+4) mod 9=3, пятый 3+4=7, шестой (7+4) mod 9=2, седьмой 2+4=6, восьмой (6+4) mod 9 = 1, девятый 1+4=5, десятый опять 5+4=9.

Итак, последовательность периодична с периодом 9. Сумма первых 9 членов равна 9+4+8+3+7+2+6+1+5=1+2+...+9=45

Сумма первых 33*9 членов 33*45=1485

Искомая сумма равна

$S_{297}+a_{298}+a_{299}+a_{300}=1485+a_1+a_2+a_3=1485+9+3+7\\=1504$

в) Т.к. 350 / 9 = 38,..., a 350 mod 9 = 8, то сумма любых 350 подряд идущих членов равна 38*45+сумма последней восьмерки. Для того, чтобы сумма была наименьшей, необходимо, чтобы наибольшее число (т.е. 9) не попало в эту восьмерку. В этом случае сумма будет равна 38*46-9=1739.

Такой случай реализется, например, при подсчете суммы членов со второго по триста пятьдесят первый.

а) 8;

б) 1504;

в) 1739, при подсчете членов, например, начиная со второго.

0,0(0 оценок)

Популярные вопросы: Математика