Видно, что левая его часть должна быть положительна. В свою очередь числитель дроби положителен. Это означает, что неравенство может быть верным только, если .
Тогда при домножении левой и правой частей неравенства на его знак сохранится.
Получим эквивалентную систему:
Преобразуем ее до более удобного вида:
(данного результата можно было добиться также и приведением дроби к общему знаменателю; рассматриванием двух случаев; исключением одного)
Построим решения всех неравенств записанной выше системы в координатах (x; a):
(см. прикрепленный файл | выделено синим)
Рассмотрим вторую строку системы:
Преобразуем ее:
Приведем систему к более удобному виду:
Построим решения всех неравенств записанной выше фразы в координатах (x; a):
(см. прикрепленный файл | выделено фиолетовым)
Будем двигать горизонтальную прямую до тех пор, пока не добьемся требуемого результата.
(см. прикрепленный файл | выделено оранжевым)
Тогда понятно, что достаточно решить систему:
Откуда следует, что при исходная система неравенств имеет единственное решение .
(см. объяснение)
Пошаговое объяснение:
Рассмотрим сначала первое неравенство системы:
Видно, что левая его часть должна быть положительна. В свою очередь числитель дроби положителен. Это означает, что неравенство может быть верным только, если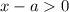
.
Тогда при домножении левой и правой частей неравенства на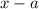
его знак сохранится.
Получим эквивалентную систему:
Преобразуем ее до более удобного вида:
(данного результата можно было добиться также и приведением дроби к общему знаменателю; рассматриванием двух случаев; исключением одного)
Построим решения всех неравенств записанной выше системы в координатах (x; a):
(см. прикрепленный файл | выделено синим)
Рассмотрим вторую строку системы:
Преобразуем ее:
Приведем систему к более удобному виду:
Построим решения всех неравенств записанной выше фразы в координатах (x; a):
(см. прикрепленный файл | выделено фиолетовым)
Будем двигать горизонтальную прямую до тех пор, пока не добьемся требуемого результата.
(см. прикрепленный файл | выделено оранжевым)
Тогда понятно, что достаточно решить систему:
Откуда следует, что при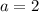
исходная система неравенств имеет единственное решение 
.
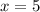Задание выполнено!
1) Опустим перпендикуляры из вершин В и С.
ВК⊥AD и CM⊥AD
2) Рассмотрим ΔАВК.
∠ВАК = 60° по условию;
∠АКВ = 90° по построению;
∠АВК = 180° - (90°+60°) = 30°
2) Катет АК против угла 30°, потому он равен половине гипотенузы АВ.
АК = 10 см : 2 = 5см
3) По построению ВК⊥AD и CM⊥AD, значит,
KBCM - прямоугольник ==> BC = KM = 6 см
ВК = СМ
4) АМ = АК + КМ
АМ = 5см + 6см = 11см
5) МD = АD - АК
МD = 16см - 11см = 5см
6) Если AK = MD = 5см,
∠AKB = ∠BMD = 90°
ВК = СМ
значит, ΔАВК = ΔCDM => AB = CD => ABCD - равнобочная трапеция => значит её диагонали равны между собой.
7) ΔАВК -прямоугольный, значит, можно применить теорему Пифагора.
АК² + ВК² = АВ²
ВК² = 10² - 5²
ВК =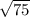
ВК = СМ =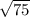
7) ΔАСМ -прямоугольный. По теореме Пифагора найдем АС.
АС² = АМ² + СМ²
АС² = 11² + (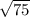
)²
АС =
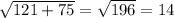см
АС = 14 см
8) AC = BD = 14см
ответ: 14см; 14см