Заметим, что сумма цифр числа дает такой же остаток при делении на 3, что и само число (разность между числом abcd... и суммой его цифр a + b + c + d + ... равна 9999...9a + 999...9b + 99...9c + 9...9d и поэтому делится на 3). Если число даёт остаток 1 при делении на 3, то следующее полученное число будет давать остаток 2 при делении на 3. Если число даёт остаток 2 при делении на 3, то следующее полученное число будет давать такой же остаток, что и 2 + 2 = 4, т.е. 1.
Исходное число даёт остаток 2 при делении на 3, тогда потом получится число с остатком 1, затем опять 2, потом 1, и т.д. Значит, число, делящееся на 3 (например, 3333) из него при загадочного калькулятора получить нельзя.
A₁=134; A₂=224; A₃=314; A₄=404
Пошаговое объяснение:
Пусть трёхзначное число A состоит из цифр x, y и z, то есть: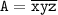
. Так как x первая цифра трёхзначного числа, то x≥1.
По первому условию: x+y+z=8. По второму условию: z=y+x. Если последнее подставит в предыдущее уравнение, то получим:
x+y+(y+x)=8 ⇔ 2·(y+x)=8 ⇔ y+x=4 ⇒ z=y+x=4.
Отсюда следует, что мы должны рассматривать трёхзначные числа, в которых последняя цифра 4: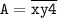
и y=4-x.
Перебираем все варианты первой цифры:
x=1 ⇒ y=4-1=3 ⇒ A₁=134;
x=2 ⇒ y=4-2=2 ⇒ A₂=224;
x=3 ⇒ y=4-3=1 ⇒ A₃=314;
x=4 ⇒ y=4-4=0 ⇒ A₄=404.
Вот и все варианты.
Заметим, что сумма цифр числа дает такой же остаток при делении на 3, что и само число (разность между числом abcd... и суммой его цифр a + b + c + d + ... равна 9999...9a + 999...9b + 99...9c + 9...9d и поэтому делится на 3).
Если число даёт остаток 1 при делении на 3, то следующее полученное число будет давать остаток 2 при делении на 3.
Если число даёт остаток 2 при делении на 3, то следующее полученное число будет давать такой же остаток, что и 2 + 2 = 4, т.е. 1.
Исходное число даёт остаток 2 при делении на 3, тогда потом получится число с остатком 1, затем опять 2, потом 1, и т.д. Значит, число, делящееся на 3 (например, 3333) из него при загадочного калькулятора получить нельзя.