Саяхатшылар 4 байдаркаға 10 адамнан отырып, өзғн бойымен төмен түсті. Оларға тағы 9 адам қосылды да жағаға қайықпен жүзді. Сонда жеті орындық неше қайық қажет?
Геометри́ческое те́ло — связная часть пространства, ограниченная замкнутой поверхностью своей наружной границы. Геометрическое тело можно определить замкнутой поверхностью, которая будет являться его границей. Геометрическим телом называют также компактное множество точек, и две точки из множества можно соединить отрезком, который целиком будет проходить внутри границы тела, что указывает на состояние геометрического тела из множества внутренних точек.
Наружная граница геометрического тела называется гранью, тело может иметь одну или множество граней. Множество плоских граней определяет множество вершин и ребер геометрического тела. Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости[1].
Примеры тел вращения Шар — образован полукругом, вращающимся вокруг диаметра разреза Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон
За площадь боковой поверхности цилиндра принимается площадь его развертки: Sбок = 2πrh.
Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов
За площадь боковой поверхности конуса принимается площадь её развертки: Sбок = πrl Площадь полной поверхности конуса: Sкон = πr(l+ r)
Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его [2]
Пошаговое объяснение:
1.
Перенесем 42 вправо, поменяв знак на противоположный, приведем подобные члены и найдем х, разделив обе части уравнения на числовой коэффициент при х:
Чтобы найти делимое, надо частное умножить на делитель:
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность:
2.
1-я сторона - ? в три раза больше 2-й;
2-я сторона - ? на 8 меньше 3-й;
3-я сторона - ?
Периметр Р=98
Пусть вторая сторона - х, тогда первая сторона - 3х, а третья - (х+8)
Периметр - сумма длин всех сторон.
Составим уравнение:
⇒ 2-я сторона - 18; 1-я сторона - 54; 3-я сторона - 26.
3.
Распределительное свойство: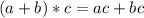
4.
Приведем подобные члены:
Геометри́ческое те́ло — связная часть пространства, ограниченная замкнутой поверхностью своей наружной границы. Геометрическое тело можно определить замкнутой поверхностью, которая будет являться его границей. Геометрическим телом называют также компактное множество точек, и две точки из множества можно соединить отрезком, который целиком будет проходить внутри границы тела, что указывает на состояние геометрического тела из множества внутренних точек.
Наружная граница геометрического тела называется гранью, тело может иметь одну или множество граней. Множество плоских граней определяет множество вершин и ребер геометрического тела. Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости[1].
Примеры тел вращения Шар — образован полукругом, вращающимся вокруг диаметра разреза Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторонЗа площадь боковой поверхности цилиндра принимается площадь его развертки: Sбок = 2πrh.
Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетовЗа площадь боковой поверхности конуса принимается площадь её развертки: Sбок = πrl Площадь полной поверхности конуса: Sкон = πr(l+ r)
Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его [2]