Щоб зробити запис у блокноті надія навмання вийняла з пиналу в якому містяться однакові за формою 4 ручки і 6 олівців.визначте ймовірність того, що вибраний нею інструмент ручка? а) 2/3 б)2/3 в)4/5 г) 3/5 (дроби)іть будь !
Частное положительного и отрицательного чисел отрицательно, так ли это: *
да+
При делении любых двух отрицательных чисел частное имеет знак:
“плюс”
Частное двух отрицательных чисел равно частному их модулей, так ли это: *
да
Укажите верные утверждения: а) частное положительного и отрицательного чисел отрицательно; б) произведение трех отрицательных чисел отрицательно; в) при умножении отличного от нуля числа на -1 получается противоположное число;
г) частное двух отрицательных чисел равно частному их модулей. *
Вспомним формулу для разложения функции в ряд Тейлора
1 Запишем функцию
2 Найдем несколько производных:
...
3 Найдем общий вид производной:
У нас в любом случае будет производная произведения, тогда наша производная распадется на какое-то количество слагаемых либо просто синуса, либо просто косинуса и слагаемое с х умноженным на либо синус, либо косинус.
Заметим, что производная синуса равна
Тогда наше произведение в зависимости от n будет иметь разный вид.
Заметим, что всего различных слагаемых без множителя х будет n штук и все они будут иметь одинаковый знак
И по содержанию, и по знаку наши функции будут одинаковые. Осталось посчитать этот знак.
При n одинаковой четности знак один и тот же, в данной точке функция имеет вид
(производная меняет местами функции)
Мы можем записать для четных n знак у функции в виде где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени
Для функции без множителя х формула такая (учитывая значения) - мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
Для функции со множителем формула другая
Чтобы избавится от ненужных двоек в первом случае, умножим все на , и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
Тогда общая формула производной имеет вид
Можем вынести множитель за скобки
4 Тогда запишем ряд Тейлора
Начинаю с 1 так как писалась формула производной от 1.
Пошаговое объяснение:
Частное положительного и отрицательного чисел отрицательно, так ли это: *
да+
При делении любых двух отрицательных чисел частное имеет знак:
“плюс”
Частное двух отрицательных чисел равно частному их модулей, так ли это: *
да
Укажите верные утверждения: а) частное положительного и отрицательного чисел отрицательно; б) произведение трех отрицательных чисел отрицательно; в) при умножении отличного от нуля числа на -1 получается противоположное число;
г) частное двух отрицательных чисел равно частному их модулей. *
а, б, в, г
Вычислите: –6,4 : 0,4 *
–16
Вычислите: (-12,8) : 4 *
-3,2
Вычислите: 5,7: (–0,3) *
-19
-253: (-11) *
23
или проще
Пошаговое объяснение:
Вспомним формулу для разложения функции в ряд Тейлора
1 Запишем функцию
2 Найдем несколько производных:
...
3 Найдем общий вид производной:
У нас в любом случае будет производная произведения, тогда наша производная распадется на какое-то количество слагаемых либо просто синуса, либо просто косинуса и слагаемое с х умноженным на либо синус, либо косинус.
Заметим, что производная синуса равна
Тогда наше произведение в зависимости от n будет иметь разный вид.
Заметим, что всего различных слагаемых без множителя х будет n штук и все они будут иметь одинаковый знак
При n одинаковой четности знак один и тот же, в данной точке функция имеет вид
(производная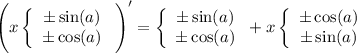 меняет местами функции)
меняет местами функции)
Мы можем записать для четных n знак у функции в виде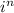 где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени
где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени 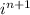
Для функции без множителя х формула такая (учитывая значения)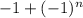 - мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
- мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
Для функции со множителем формула другая
Чтобы избавится от ненужных двоек в первом случае, умножим все на , и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
, и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
Тогда общая формула производной имеет вид
Можем вынести множитель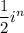 за скобки
за скобки
4 Тогда запишем ряд Тейлора
Начинаю с 1 так как писалась формула производной от 1.
f(2) = 2 * cos ( 2-2 ) = 2 * 1 = 2
Это и есть ответ