Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
Пусть , тогда .
Делаем подстановку в наше изначальное выражение:
Здесь сокращаются и мы имеем . Выносим за интеграл: . Теперь мы имеем знакомый интеграл, который равняется , тоже самое что . Подставляем и имеем . Используем фундаментальную теорему исчисления:
Пошаговое объяснение:
1)По условию :
а=х м
b=(х+4) м
S= 45 м²
Формула площади :
S=a*b можем записать уравнение:
x(4+x)=45
4х+ х²= 45
х²+4х -45=0
D=16+180=196
√196=14
х₁=( -4+√D)/2= (-4+14)/2=5
x₂= (-4-√D)/2=(-4-14)/2=-9 не подходит , поскольку отрицательный , чего не может быть
Значит одна сторона 5 м, а вторая
5+4=9 м
а= 5м , b= 9м
2) Получаем систему уравнений
5x - 3y = 17
x² + y² = 17
из первого уравнения найдем у и подставим во второе уравнение
y = (5x-17)/3
x² + ((5x-17)/3)²=17
9х² + (5x-17)²=17*9
9x² + 25x² - 170x + 289 = 153
34x²-170x+136=0
разделим на 34
x²-5x+4=0
x²-4x-x+4=0
x(x-4)-(x-4)=0
(x-4)(x-1)=0
x₁=1
x₂=4
подставим значения х и найдем у
y = (5x-17)/3
y₁=(5*1-17)/3=-4
у₂= (5*4-17)/3=1
( 1; -4) и ( 4; 1)
ответ: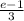
Пошаговое объяснение:
ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
Пусть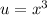 , тогда
, тогда ![x=\sqrt[3]{u}](/tpl/images/1117/3966/8c879.png) .
.
Делаем подстановку в наше изначальное выражение:
Здесь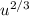 сокращаются и мы имеем
сокращаются и мы имеем 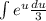 . Выносим
. Выносим 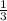 за интеграл:
за интеграл: 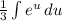 . Теперь мы имеем знакомый интеграл, который равняется
. Теперь мы имеем знакомый интеграл, который равняется 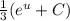 , тоже самое что
, тоже самое что 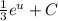 . Подставляем
. Подставляем 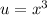 и имеем
и имеем 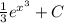 . Используем фундаментальную теорему исчисления:
. Используем фундаментальную теорему исчисления: