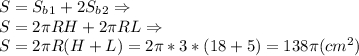У равнобедренного прямоугольного треугольника катеты равны и острые углы по 45 градусов. Прямоугольный треугольник строим из вершины. Выбираем точку (вершина), от неё в сторону и вверх откладываем равные отрезки (под прямым углом). Соединяем концы отрезков. Полученный треугольник стоит на катете.
Строим по гипотенузе (основанию). Делим её пополам, из этой точки вверх проводим перпендикуляр. Из концов основания проводим лучи под углами в 45 градусов до пересечения с перпендикуляром. Получили прямоугольный треугольник, лежащий на гипотенузе (на основании).
Построим равнобедренную трапецию ABCD с высотой CF (см. Рис. 1).
Согласно условию: AD=18 см, BC=10 см, CF=3 см. Для дальнейших вычислений нам понадобится длина боковой стороны трапеции AB=CD.
Т.к. трапеция равнобедренная, то FD = (AD-BC):2 = 4 см.
ΔCDF - прямоугольный с катетами CF=3 см, FD=4 см, значит он египетский, и его гипотенуза CD=5 см.
При вращении такой трапеции вокруг короткого основания образуется цилиндр с равными осевыми конусообразными выемками с обеих сторон (См. рис. 1.2, 2.1, 2.2). Радиус такого цилиндра равен высоте трапеции R=CF=3 см, а высота цилиндра равна длинному основанию трапеции H=AD=18 см.
Образующей конуса-выемки является боковая сторона трапеции L=CD=5 см, радиус равен радиусу цилиндра R=3 см.
Искомая площадь полной поверхности фигуры вращения состоит из площади боковой поверхности цилиндра и двух боковых поверхностей конусов-выемок.
Прямоугольный треугольник строим из вершины. Выбираем точку (вершина), от неё в сторону и вверх откладываем равные отрезки (под прямым углом). Соединяем концы отрезков. Полученный треугольник стоит на катете.
Строим по гипотенузе (основанию). Делим её пополам, из этой точки вверх проводим перпендикуляр. Из концов основания проводим лучи под углами в 45 градусов до пересечения с перпендикуляром. Получили прямоугольный треугольник, лежащий на гипотенузе (на основании).
138π см²
Пошаговое объяснение:
Построим равнобедренную трапецию ABCD с высотой CF (см. Рис. 1).
Согласно условию: AD=18 см, BC=10 см, CF=3 см. Для дальнейших вычислений нам понадобится длина боковой стороны трапеции AB=CD.
Т.к. трапеция равнобедренная, то FD = (AD-BC):2 = 4 см.
ΔCDF - прямоугольный с катетами CF=3 см, FD=4 см, значит он египетский, и его гипотенуза CD=5 см.
При вращении такой трапеции вокруг короткого основания образуется цилиндр с равными осевыми конусообразными выемками с обеих сторон (См. рис. 1.2, 2.1, 2.2). Радиус такого цилиндра равен высоте трапеции R=CF=3 см, а высота цилиндра равна длинному основанию трапеции H=AD=18 см.
Образующей конуса-выемки является боковая сторона трапеции L=CD=5 см, радиус равен радиусу цилиндра R=3 см.
Искомая площадь полной поверхности фигуры вращения состоит из площади боковой поверхности цилиндра и двух боковых поверхностей конусов-выемок.
Площадь боковой поверхности цилиндра: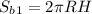 .
.
Площадь боковой поверхности конуса-выемки: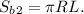
Площадь полной поверхности: