) Если квартира № 83 находится на 5 этаже, а квартир на площадке - 4, значит число кватир должно быть кратно 4 (это 84), и на 5 этаже расположены квартиры с 81 по 84, а с 1 - по 4 этажи 4*4 = 16 квартир , тогда номера квартир в предыдущем подъезде заканчиваются №64 (84-5*4) а в поъезде Олега начинаются с номера 65. 2) Первые 64 квартиры занимают 64:4=16 этажей, значит дом может быть либо 8-ми этажный, либо 16-ти - этажный (4-х этажный быть не может, т.к. Олег живет на 5 этаже)3) Предположим, что дом 16-ти этажный, тогда квартиры в подъезде Олега заканчиваются номером: 64+4*16=128, а в следующем подъезде начинаются с номера 129, но тогда квартира Насти будет находитьмся на (169-129):4+1=11 этаже, а это противоречит условию, следовательно дом - 8-ми этажный.4) Олег и Настя живут в 8-ми этажном доме. В 1-ом подъезде - номера квартир с 1 по 32, во 2-ом подъезде с 33 по 64, в 3-ем подьезде с 65 по 96, в 4-ом - с 97 по 128, в 5-ом подъезде с 129 по 160, в 6-ом подъезде - 1 этаж (кв.№161-164); 2-ой этаж (кв.№165-168); на 3-ем этаже в кв. №169 - живет Настя.
Найдем сначала общее решение соответствующего однородного дифференциального уравнения
Пусть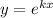 , мы получим характеристическое уравнение
, мы получим характеристическое уравнение
Найдём теперь частное решение. Рассмотрим функцию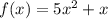
Подставляем в исходное дифференциальное уравнение
Приравниваем коэффициенты при степени x
Частное решение: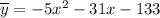
Общее решение линейного неоднородного дифференциального уравнения: