Изучаемый прямоугольный треугольник имеет катеты и и гипотенузу (чертеж в приложении).
При этом, третья сторона была вычислена по теореме Пифагора: .
Из этого следует, что вращали треугольник вокруг катета, равного (это есть больший катет, ).
При вращении прямоугольного треугольника вокруг одного из катетов, как известно, получается конус. В данном случае его высота равна , радиус основания и образующая .
Для вычисления полной поверхности конуса используем соответствующую формулу:
Из точки B проводим биссектрису (BD=4см), которая делит угол пополам.
Из точки D опускаем перпендикуляры на стороны AB и BC.Получатся отрезки DE и DF.
Образовалось два прямоугольных треугольника BDE и BDF, в которых угол B равен 30 град. (угол 60 град. разделен пополам).
Согласно правилу, катет, который лежит напротив угла равного 30 град. равен половины гипотенузы.
У нас гипотенуза равна 4 см (BD).
Следовательно расстояния до сторон угла (у нас это отрезки DE и DF) равны 2 см.
Изучаемый прямоугольный треугольник имеет катеты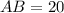
и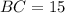 
и гипотенузу 
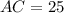(чертеж в приложении).
При этом, третья сторона была вычислена по теореме Пифагора:Из этого следует, что вращали треугольник вокруг катета, равного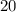
(это есть больший катет, 
).
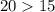При вращении прямоугольного треугольника вокруг одного из катетов, как известно, получается конус. В данном случае его высота равна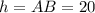
, радиус основания 
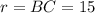и образующая 
.
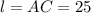Для вычисления полной поверхности конуса используем соответствующую формулу:
Подставляем известные значения:
ответ: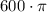
или около 
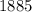(ед³).