Воспользуемся формулой приведения:
Зная, что выполним отбор корней.
Для первой серии:
Для второй серии:
ответ: 4 корня
Воспользуемся формулой приведения:
Зная, что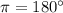 выполним отбор корней.
выполним отбор корней.
Для первой серии:
Для второй серии:
ответ: 4 корня