Для трехзначного числа вместо цифры может стоять одна из двух цифр: 3 или 6 (цифра 0 не может находится в наивысшем разряде в трехзначном числе); вместо цифры может стоять одна из двух оставшихся цифр, включая 0; вместо цифры может стоять одна оставшаяся цифра.
Таким образом, по правилу комбинаторного произведения имеем таких трехзначных числа.
Из 3 цифр можно образовать 3 перестановки . Однако трехзначное число не может начинаться с нуля. Перестановки, начинающиеся с цифры 0, а следовательно, не удовлетворяющие условию задачи, будет . Итак, искомое количество трехзначных чисел равно:
В) 4
Пошаговое объяснение:
1-ый
На первую позицию можно подставить любую цифру, кроме 0 (т.к на 0 число не может начинаться) - 2.
На вторую позицию можно подставить оставшуюся цифру и 0 (ноль) - 2.
На третью позицию можно подставить 1 оставшуюся цифру - 1.
2*2*1=4*1=4 числа
Для трехзначного числа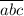
вместо цифры 
может стоять одна из двух цифр: 3 или 6 (цифра 0 не может находится в наивысшем разряде в трехзначном числе); вместо цифры 
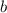может стоять одна из двух оставшихся цифр, включая 0; вместо цифры 
может стоять одна оставшаяся цифра.
Таким образом, по правилу комбинаторного произведения имеем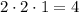
таких трехзначных числа.
Из 3 цифр можно образовать 3 перестановки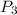
. Однако трехзначное число не может начинаться с нуля. Перестановки, начинающиеся с цифры 0, а следовательно, не удовлетворяющие условию задачи, будет 
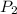. Итак, искомое количество трехзначных чисел равно:
ответ: 4