Сколько существует шестизначных десятичных чисел, если в каждом числе цифры расположены в порядке возрастания и если каждое число начинается с единицы и оканчивается девяткой

2 задание.

1)натуральные:

9,  24

2)целые:

9,-16,0,24,-50

3)положительные:

9; 1/19 ; 7,2; 4 3/16 ; 24

4)целые отрицательные:

-16, -50

5)дробные отрицательные:

-3,8; -2 6/17

Задание 3.

1)3,1> -6,7

2)-4,2> -4,6

Задание 4.

1)7,3+1,8-3,45 = 5,65 ( модуль раскрывается со знаком + )

2)17/90 : 1 8/9 =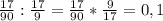

Задание 5.

1)если -х = 25,то х = -25

2)если -(-х)= - 4,9 , то х = -4,9

Задание 6.

1)модуль х = 4,5

х = ±4,5

2)модуль х = -1,8

Такого быть не может,т.к. любое число в модуле положительное,либо равно 0.

Задание 7.

х > -14

Наименьшее целое значение равно

x= -13

Задание 8.

-5,35* < -5,356

Вместо звездочки можно поставить цифры 5,4,3,2,1,0

Задание 9.

Нужно найти такие числа х,которые

- 0,35294117647 < x < - 0,29411764705

Тогда х = - 0,34 и х = -0,33

1
а) Вероятность сдать экзамен - дано - p1=0,6, р2=0,5, р3=0,8.
Вероятность провалить = не сдать -  q1=1-p1=0.4, q2=0.5, q3=0.2
Вероятности событий "И" - умножаются, а событий "ИЛИ" - суммируются.
Формула словами - (И да1 И да2 И не3) ИЛИ (И да1 И не2 И да3) ИЛИ (И не1 И да2 И да3).
Вероятность сдать два из трех по формуле:
P(A)=p1*p2*q3 + p1*q2*p3 = q1*p2*p3 = 0.6*0.5*0.2 + 0.6*0.5*0.8 + 0.4*0.5*0.8 = 0.06+0.24+0.16 = 0.46 = 46% - ОТВЕТ
б) два или даже три сдаст - добавляем вероятность всех трех экзаменов.
Р(В) = Р(А) + р1*р2*р3 = 0,46 + 0,6*0,5*0,8 = 0,46+0,24=0,7= 70% - ОТВЕТ
2. Два события - вероятность выплаты и вероятность страхового случая.
а) Р = 0,15 *  3/10 = 0,045 = 4,5% - ОТВЕТ
б) Р = 0,15 * 80/300 ~ 0,15*0,2667 = 0.04 = 4% - ОТВЕТ