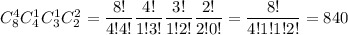Если число делится на 2, то его последняя цифра четна. Среди цифр числа 131152152 из четных цифр присутствует лишь цифра 2. Она и будет стоять на последнем месте.
Осталось 8 мест и цифры: 1 - 4 штуки, 2 - 1 штука, 3 - 1 штука, 5 - 2 штуки.
А значит число искомых чисел равно числу упорядоченных разбиений множества из 8 мест на 4 множества мощности 4, 1, 1 и 2 (каждому множеству соответствует одна из цифр 1, 2, 3 или 5), т.е. числу перестановок с повторениями
____________________________________
Последняя формула может быть получена следующими рассуждениями:
сначала расставим 4 единицы на каких-то из свободных 8 мест. Сделать это можно Незанятыми остались 8-4=4 места. На этих 4 местах расставим 1 двойку. Сделать это можно И т.д.
840
Пошаговое объяснение:
Если число делится на 2, то его последняя цифра четна. Среди цифр числа 131152152 из четных цифр присутствует лишь цифра 2. Она и будет стоять на последнем месте.
Осталось 8 мест и цифры: 1 - 4 штуки, 2 - 1 штука, 3 - 1 штука, 5 - 2 штуки.
А значит число искомых чисел равно числу упорядоченных разбиений множества из 8 мест на 4 множества мощности 4, 1, 1 и 2 (каждому множеству соответствует одна из цифр 1, 2, 3 или 5), т.е. числу перестановок с повторениями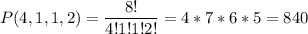
____________________________________
Последняя формула может быть получена следующими рассуждениями:
сначала расставим 4 единицы на каких-то из свободных 8 мест. Сделать это можно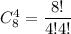 Незанятыми остались 8-4=4 места. На этих 4 местах расставим 1 двойку. Сделать это можно
Незанятыми остались 8-4=4 места. На этих 4 местах расставим 1 двойку. Сделать это можно 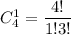 И т.д.
И т.д.
По правилу произведения кол-во чисел равно