Скорость автомобиля и время его движения обратно пропорционально да или нет

Показать ответ

Ответ:

Monika950

26.03.2021 22:40

Пошаговое объяснение:

a) 56 + 27 = 83

б) 320 + 715 = 1035

в) 1516 - 34 = 1482

г) 1316 - 712 = 604

д) 25 + 13 - 730 = -692

25 + 14 + 58 + 35 + 34 + 38 = (25 + 35) + (58 + 38 + 14) + 34 = 60 + 110 + 34 = 204

1) 360 * 4/9 = 160 (кг) - картофеля

2) 360 * 7/24 = 105 (кг) - моркови

3) 360 - 160 - 105 = 95 (кг) - капусты

ответ: в магазин завезли 95 кг капусты.

1) 1 - 7/15 = 15/15 - 7/15 = 8/15 (книг) - завезли во 2-ой день

2) 56 * 15/8 = 7 * 15 = 105 (книг) - завезли за 2 дня

ответ: за 2 дня в библиотеку завезли 105 книг

а)

x + 18 = 35

x = 35 - 18

x = 17

б)

x - 37 = 421

x = 421 + 37

x = 458

Надеюсь, смогла чем-нибудь ))

0,0(0 оценок)

Ответ:

d180902

03.02.2023 02:35

Я могу дать только одну интерпретацию условия: доказать, что число 2528 нельзя представить в виде суммы

a_1^6+a_2^6+a_3^6+a_4^6+a_5^6+a_6^6+a_7^6,

где $a_1,\ a_2,\ a_3,\ a_4,\ a_5,\ a_6,\ a_7\ -$ целые числа. Такую задачу я и буду решать.

Поскольку шесть четное число, достаточно доказать утверждение для неотрицательных целых чисел. Имеем:

$0^6=0;\ 1^6=1;\ 2^6=64;\ 3^6=729;\ 4^6=40962528\Rightarrow n^62528$

при n>3. Поэтому надо пытаться делать 2528 из чисел 0, 1, 64 и 729.

Если использовать только первые три числа, то сумма будет не больше чем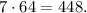 $7 \cdot 64=448.$ До 2528 мы не дотянули на 2528-448=2080 единиц. Значит, надо использовать и 729, причем поскольку

2080:729=2,8... , 729 нужно использовать как минимум 3 раза, а поскольку 729·4=2916>2528, число 729 нужно использовать ровно 3 раза. Теперь задача сводится к более простой:

2528-729·3=2528-2187=341; число 341 нужно представить в виде суммы четырех чисел, используя только 0, 1, и 64. Однако такая сумма заведомо не может быть больше, чем 4·64=256.

Следовательно, мы доказали, что число 2528 нельзя представить в виде суммы семи шестых степеней целых чисел.

0,0(0 оценок)

Популярные вопросы: Математика