Заметим, что для того чтобы существовало одно решение на интервале (0;π/2), необходимо и достаточно, чтобы выполнялось условие , в этом случае на промежутке (0;π/2) будет существовать ровно ОДНО значение x, в противном случае, решений на данном промежутке не будет.
Откуда, должно выполнятся условие:
По условию, нужно найти те значения параметра a, при которых будет более одного решения на интервале (0;π/2), а значит данное уравнение должно иметь как минимум два положительных решения.
1)
Рассмотрим линейный случай, ибо может быть бесконечное число решений:
- одно решение
2) Основной случай.
Должно быть два корня, каждый из которых больше единицы :
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем k,\,n\in Z (на всякий случай, эта запись означает, что числа n и k принадлежат множеству целых чисел):
\[ 4x+\frac{\pi}{4}=\pm\operatorname{arccos \left(-\frac{\sqrt{2}}{2}\right)}+2\pi k. \]
Арккосинус a есть число, заключенное в интервале от 0 до \pi, косинус которого равен a.
Арксинус a есть число, заключенное в интервале от -\pi до \pi, косинус которого равен a.
Другими словами, нам нужно подобрать такое число из промежутка [0;2\pi], косинус которого был бы равен -\frac{\sqrt{2}}{2}. Это число \frac{3\pi}{4}. Используя это, получаем:
ответ: a∈(-1;-2/3) ∪ (-2/3 ; -1/3)
Пошаговое объяснение:
ОДЗ: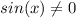
Используем формулу:
Замена: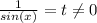
Заметим, что для того чтобы существовало одно решение на интервале (0;π/2), необходимо и достаточно, чтобы выполнялось условие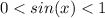 , в этом случае на промежутке (0;π/2) будет существовать ровно ОДНО значение x, в противном случае, решений на данном промежутке не будет.
, в этом случае на промежутке (0;π/2) будет существовать ровно ОДНО значение x, в противном случае, решений на данном промежутке не будет.
Откуда, должно выполнятся условие: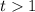
По условию, нужно найти те значения параметра a, при которых будет более одного решения на интервале (0;π/2), а значит данное уравнение должно иметь как минимум два положительных решения.
1)
Рассмотрим линейный случай, ибо может быть бесконечное число решений:
2) Основной случай.
Должно быть два корня, каждый из которых больше единицы :
a∈(-1;-2/3) ∪ (-2/3 ; -1/3)
Решение простейших тригонометрических уравнений
Пример 1. Найдите корни уравнения
\[ \cos\left(4x+\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}, \]
принадлежащие промежутку [-\pi;\pi).
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем k,\,n\in Z (на всякий случай, эта запись означает, что числа n и k принадлежат множеству целых чисел):
\[ 4x+\frac{\pi}{4}=\pm\operatorname{arccos \left(-\frac{\sqrt{2}}{2}\right)}+2\pi k. \]
Арккосинус a есть число, заключенное в интервале от 0 до \pi, косинус которого равен a.
Арксинус a есть число, заключенное в интервале от -\pi до \pi, косинус которого равен a.
Другими словами, нам нужно подобрать такое число из промежутка [0;2\pi], косинус которого был бы равен -\frac{\sqrt{2}}{2}. Это число \frac{3\pi}{4}. Используя это, получаем:
\[ 4x+\frac{\pi}{4} = \pm\frac{3\pi}{4}+2\pi k\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{8}+\frac{\pi k}{2}, \\ x = -\frac{\pi}{4}+\frac{\pi n}{2}.\end{array}\right. \]