Сначала, раскроем первую скобку, умножив то число, которое находится сразу перед скобкой, на каждое число в скобке, учитывая знаки. Вторую скобку можно просто убрать, но если перед ней есть знак «–», то все знаки чисел поменяются:
0,5(8x + 1) = 1,5 – (9 – 4x)
4х + 0,5 = 1,5 – 9 + 4х
Числа с «х» переведём на левую сторону, без «х» — на правую. Переведённое на противоположную сторону число поменяет свой знак.
4х + 0,5 = 1,5 – 9 + 4х
4х – 4х = 1,5 – 9 – 0,5
0х = 0
х ∈ ∞
(∞ — уравнение имеет бесконечное количество корней. Уравнение имеет бесконечное количество корней, когда и коэффициент переменной равен 0, и правая сторона равна 0)
Сначала, раскроем первую скобку, умножив то число, которое находится сразу перед скобкой, на каждое число в скобке, учитывая знаки. Вторую скобку можно просто убрать, но если перед ней есть знак «–», то все знаки чисел поменяются:
0,5(8x + 1) = 1,5 – (9 – 4x)
4х + 0,5 = 1,5 – 9 + 4х
Числа с «х» переведём на левую сторону, без «х» — на правую. Переведённое на противоположную сторону число поменяет свой знак.
4х + 0,5 = 1,5 – 9 + 4х
4х – 4х = 1,5 – 9 – 0,5
0х = 0
х ∈ ∞
(∞ — уравнение имеет бесконечное количество корней. Уравнение имеет бесконечное количество корней, когда и коэффициент переменной равен 0, и правая сторона равна 0)
Пошаговое объяснение:
Пусть SABC -правильная треугольная пирамида.
S(бок)=3S(осн)
Так как пирамида правильная, то треугольник АВС - правильный. Пусть сторона треугольника будет а.
Тогда площадь основания буден равна
S(бок)=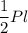 , где Р- периметр основания, а
, где Р- периметр основания, а 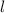 - апофема.
- апофема.
Так как площадь боковой поверхности в 3 раза больше площади основания, то
Рассмотрим треугольник SOM - прямоугольный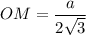 , как радиус окружности , вписанной в правильный треугольник АВС.
, как радиус окружности , вписанной в правильный треугольник АВС.
Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Объем пирамиду определяется по формуле:
где площадь основания, а Н - высота пирамиды.
площадь основания, а Н - высота пирамиды.
Значит, объем пирамиды равен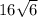 куб. ед.
куб. ед.