Составить канонические уравнения: а) эллипса; б) гиперболы; в)параболы ( A, B – точки, лежащие на кривой, F – фокус, a – большая (действительная) полуось, b – малая (мнимая) полуось, е – эксцентриситет, y = +-kx – уравнение асимптот гиперболы, D – директриса кривой, 2c – фокусное расстояние). Если а) b = 2, е = 5*корень29/29; б)k = 12/13, 2a = 16; в)ось симметрии Ox и A(-5,15).

Показать ответ

Ответ:

впнекккккк

26.03.2021 04:36

Пусть первое число арифметической прогресии равно а, тогда второе будет а + d, третье а +2d. Сумма а + а + d + а + 2d = 12

3а + 3d = 12

а + d = 4, следовательно а = 4 - d,

а + d = 4 (это второе число арифметической прогрессии)

при увеличении первого числа на 1, второго на 2 и третьего на 11 они составляют геометрическую прогрессию: 5-d; 6; 15+d.

Составим уравнение: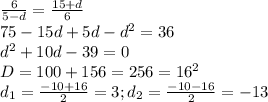 $\frac{6}{5-d}=\frac{15+d}{6}\\75-15d+5d-d^{2}=36\\d^{2}+10d-39=0\\D=100+156=256=16^{2}\\d_{1}=\frac{-10+16}{2}=3;d_{2}=\frac{-10-16}{2}=-13$

Так как арифметическая прогрессия убывающая, то подходит корень уравнения -13. Значит, первое число будет 4 - (-13) = 17; второе 4; третье 4 - 13 = -9.

Составим РС: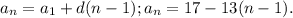 $a_{n}=a_{1}+d(n-1);a_{n}=17-13(n-1).$ - это арифметическая прогрессия.

Найдем РС для геометрической прогрессии: 18; 6; 2.

$b_{1}=18;q=\frac{1}{3}\\b_{n}=b_{1}\cdot{q^{n-1}}\\b_{n}=18\cdot{(\frac{1}{3})^{n-1}}$

0,0(0 оценок)

Ответ:

НастяМосква13

26.03.2021 04:36

Пусть одно число равно х, тогда второе число будет (12-х). Т. к. произведение этих чисел равно 11, то составим и решим уравнение
х(12-х)=11,
12х-х²=11,
-х²+12х-11=0,
х²-12х+11=0.
D=b²-4ac=(-12)²-4·1·11=144-44=100; √100=10.
х1=(12+10)/2=11, х2=(12-10)/2=1.
Значит, это числа 1 и 11.

Если все таки это -11, о получим уравнение х²-12х-11=0.
D=b²-4ac=(-12)²-4·1·(-11)=144+44=188; √188=√(4*47)=2√47.
х1=(12+2√47)/2=6+√47
х2=(12-2√47)/2=6-2√47
Значит, первое число равно 6+√47 или 6-√47, тогда второе числобудет равно:
12-(6+√47)=6-√47 или 12-(6-√47)=6+√47.

0,0(0 оценок)

Популярные вопросы: Математика