Даны точки М1 (1; 2) и М2 (3; 7).
Подставим эти координаты в уравнение гиперболы.
Получаем уравнение
Замена: подставим значение b^2 в первое уравнение.
(1/a^2) -(4/(45/8)a^2) = 1.
Отсюда находим a^2 = 13/45, а b^2 = (45/8)*(13/45) = 13/8.
ответ: уравнение гиперболы (x^2/(13/45)) - (y^2/(13/8)) = 1.
Параметры гиперболы и график приведены во вложении.
Даны точки М1 (1; 2) и М2 (3; 7).
Подставим эти координаты в уравнение гиперболы.
Получаем уравнение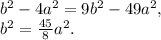
Замена: подставим значение b^2 в первое уравнение.
(1/a^2) -(4/(45/8)a^2) = 1.
Отсюда находим a^2 = 13/45, а b^2 = (45/8)*(13/45) = 13/8.
ответ: уравнение гиперболы (x^2/(13/45)) - (y^2/(13/8)) = 1.
Параметры гиперболы и график приведены во вложении.