Пошаговое объяснение:
Уравнение касательной к функции f(x) в точке x₀
где - значение производной функции f(x) в точке x₀ .
Для данной задачи
Тогда
После раскрытия скобок и приведения подобных
Пошаговое объяснение:
Уравнение касательной к функции f(x) в точке x₀
где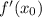 - значение производной функции f(x) в точке x₀ .
- значение производной функции f(x) в точке x₀ .
Для данной задачи
Тогда
После раскрытия скобок и приведения подобных