Спроецируем прямую АВ на плоскость ХОZ и получим прямую А1В1. Это будет след заданной плоскости, параллельной оси ОУ. Тангенс угла наклона к оси ОХ равен (3-(-1))/(-3-2) = -4/5. Находим отрезки на осях координат, отсекаемые искомой плоскостью. Возьмём точку В1 на прямой А1В1. Она пересекает ОХ на расстоянии 3/(-4/5) = -15/4 = -3,75 от проекции точки В1 на ось ОХ. -3-(-3,75) =0,75 = 3/4. На оси OZ точка пересечения равна 0-(0,75*(-4/5) = 0,6 = 3/5.
Если плоскость пересекает оси OX, OY и OZ в точках с координатами (a, 0, 0), (0, b, 0) и (0, 0, с), то она может быть найдена, используя формулу уравнения плоскости в отрезках
Ось ОУ не пересекается, то есть b=0 и это слагаемое отсутствует. Подставим значения отрезков в уравнение: После преобразования получим уравнение плоскости:
Это будет след заданной плоскости, параллельной оси ОУ.
Тангенс угла наклона к оси ОХ равен (3-(-1))/(-3-2) = -4/5.
Находим отрезки на осях координат, отсекаемые искомой плоскостью.
Возьмём точку В1 на прямой А1В1. Она пересекает ОХ на расстоянии 3/(-4/5) = -15/4 = -3,75 от проекции точки В1 на ось ОХ.
-3-(-3,75) =0,75 = 3/4.
На оси OZ точка пересечения равна 0-(0,75*(-4/5) = 0,6 = 3/5.
Если плоскость пересекает оси OX, OY и OZ в точках с координатами (a, 0, 0), (0, b, 0) и (0, 0, с), то она может быть найдена, используя формулу уравнения плоскости в отрезках
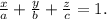
Ось ОУ не пересекается, то есть b=0 и это слагаемое отсутствует.Подставим значения отрезков в уравнение:
После преобразования получим уравнение плоскости: