Составить уравнение плоскости, проходящую через точку к (1,5,2) и параллельна плоскости, проходящую через 3 точки: l(4,-3,1), m(3,4,0), n(-1,-1,5)

как правильно решить найдем плоскость с уравнения плоскости, проходящую через 3 точки.
x-4 y+3 z-1
3-4 4+3 0-1 0
-1-4 -1+3 5-1

x-4 y+3 z-1
-1 7 -1 0
-5 2 4

30x+9y+33z-126=0

ax+by+cz+d=0
30*1+9*5+33*2 = 141

значит уравнение плоскости: 30x+9y+33z -141 = 0 или 30х+9у+33z+141=0
(плюс или минус перед 141 точно не знаю найдем вектора
lm (-1,7,-1), ln (-5,4,4), lk (-3,8,1)

х+1 у-7 z+1
-5+1 4-7 4+1 ===0
-3+1 8-7 1+1

-11x-2y-10z-7=0

Сочинение описание: Крым

Далеко в море уходит большой участок суши – полуостров Крым. Природа его удивительная! Южную часть занимает степь, на крайнем юге пролегают горы, которые спускаются просто к морю. Крымские горы сравнительно невысокие и тянутся на 150 км. Высочайшая вершина Крыма гора Роман-Кош – имеет высоту 1545 м. Между горами и морем тянется полоса побережья – Южный берег Крыма. Горы защищают этот уголок от северных ветров, а море смягчает жару. Это самый теплый регион страны.

Здесь очень благоприятный климат – весна наступает в феврале, а безморозный период превышает 220 дней. По количеству солнечных дней Крым занимает одно из первых мест в Восточной Европе! Разнообразна и растительность полуострова. Шиповник, ежевика, боярышник вместе со скумпией, ладаном и другими кустами образуют непролазные заросли. Обычными для этих мест являются дубы. Кое-где сохранились типично средиземноморские рощи, которые состоят из можжевельника, сосны Станкевича, фисташки туполистой. На открытой местности властвуют группировки южных сухолюбивых растений наподобие астрагала, кермека. Выше в горах появляются леса, которые состоят из крымской сосны и других различных видов деревьев. На высоте 1000 1300 м растут большие дубы, буковые и смешанные леса, а также сосна крымская. Еще выше, на вершинах со сглаженным рельефом начинаются лугостепи. В горах Крыма количество осадков доходит до 1100 мм. Вот почему здесь растет бук – довольно влаголюбивая порода дерева. все что нашел извини

Единственно возможный вариант - 17, 5.

Пошаговое объяснение:

Обозначим числа как и .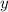

Если сумма двух чисел - чётное число, то чётность искомых чисел одинакова, то есть или оба числа чётные или оба нечётные.

Но если числа одинаковой чётности, то разность будет тоже чётной. Между 10 и 14 только 1 чётное число - это 12, так как мы не считаем 10 и 14.

Теперь составляем систему уравнений:

Сложим уравнения:

Упростим правую часть:

Упростим левую часть:

И ещё раз её упростим:

Теперь легко найти :

Находим :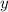

Вывод: Единственный возможный вариант - 17, 5.

УДАЧИ! ОБРАЩАЙТЕСЬ!