Составьте квадратное уравнение с целыми коэффициентами, корни
которого равны:
1. 2 и 5
2. -1/3 и 2
3. -0,2 и -10
4. 2 - корень 3 и 2 + корень 3
5. 0 и 6
6. - корень 7 и корень 7

Показать ответ

Ответ:

Женя220V

10.03.2021 11:25

Номер √1

a)7/9+4/6=14/18+12/18=26/18=13/9=1,4/9

b)5/7-8/10=50/70-56/70=-6/70=-3/35

c)1/2+(3/7-0,45)=1/2+(300/700-315/700)=1/2+(-15/700)=1/2+(-3/140)=70/140+(-3/140)=67/140

Номер √2

Сначала мы должны привести их к общему знаменателю :

4/7 и 7/12 из общий знаменатель 84

первая доска 48/84 метра а вторая доска 49/84 .Значит вторая доска длинее на 1/84 метра

Номер√3

а) x=5/4-1/3=15/12-4/12=11/12

b)x=5/18+1/7=35/126+18/126=53/126

Номер √6

то же самое делаем как во втором задаче 3/8=6/16 + 2/16=16/16-8/16=8/16=1/2

ответ:они работали 1/2 время

0,0(0 оценок)

Ответ:

elenanovikova1972

15.02.2022 19:06

Пошаговое объяснение:

Для удобства набора решения, все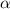 $\alpha$ я заменил на

Сначала предварительная подготовка:

$\sin^4(x) + \cos^4(x) = (\sin^2(x) + \cos^2(x))^2 - 2\sin^2(x)\cos^2(x) = 1^2 - 2\sin^2(x)\cos^2(x)$ .

То есть

$\sin^4(x) + \cos^4(x) = 1^2 - 2\sin^2(x)\cos^2(x)$ (в цепочке равенств оставил только первый и последний член).

Значит после переноса получаем:

$1 - \sin^4(x) - \cos^4(x) = 2\sin^2(x)\cos^2(x)$ .

Теперь работаем с числителем.

$\sin^6(x) + \cos^6(x) = (\sin^2(x) + \cos^2(x))^3 - 3\sin^4(x)\cos^2(x) - 3\sin^2(x)\cos^4(x) = 1^3 - 3\sin^2(x)\cos^2(x)(\sin^2(x)+\cos^2(x)) = 1 - 3\sin^2(x)\cos^2(x)$ .

Значит

$1 - \sin^6(x) - \cos^6(x) = 3\sin^2(x)\cos^2(x)$ .

Осталось самое приятное: подставить наши результаты в дробь, и понять, что всё получилось

$\frac{1 - \sin^4(x) - \cos^4(x)}{1 - \sin^6(x) - \cos^6(x)} = \frac{3\sin^2(x)\cos^2(x)}{2\sin^2(x)\cos^2(x)} = \frac{3}{2}$

ч.т.д.

Перемножим дробь "крест-накрест", получим:

$(\sqrt{3} - 2\sin(x))(\sqrt{3} + 2\sin(x)) = (2\cos(x) - 1)(2\cos(x) + 1)$

по формуле разностти квадратов, получаем:

$3 - 4\sin^2(x) = 4\cos^2(x) - 1$

переносим в одну часть

$4 = 4(\sin^2(x) + \cos^2(x))$ ,

что верно в силу основного тригонометрического тождества. Так как мы тождественными преобразованиями перешли от исходного выражения к тождественному равенству, значит изначально тоже было тождественное равенство, ч.т.д.

0,0(0 оценок)

Популярные вопросы: Математика