Пусть из некоторого города A нельзя попасть в некоторый город B по а1. Рассмотрим множество M всех городов, в которые можно попасть из города A по а1. Множество городов, не входящих в M, обозначим N. Множество N непусто, поскольку в нём содержится город B. Ясно, что из городов множества M нельзя попасть в города множества N по а1.
Докажем, что из каждого города в любой другой можно попасть по а2.
Если один из городов принадлежит M, а другой – множеству N, то между ними есть прямая авиалиния а2.
Пусть два города принадлежат M. Тогда из первого города можно попасть по а2 в некоторый город множества N, а оттуда (также по а2) – во второй город.
Аналогично рассматривается случай, когда оба города принадлежат N.
ИССЛЕДОВАНИЕ 1. Область определения. Деление на ноль в знаменателе. Х≠ 1. Х∈(-∞;0)∪(0;+∞) 2. Вертикальная асимптота: Х= 1. 3. Пересечение с осью Х. Y(x) = 0 - нет. 4. Пересечение с осью У - нет 5. Наклонная асимптота k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность. Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x) Функция ни четная ни нечетная. 7. Поведение в точке разрыва. lim(->0-) Y(x) = -∞. lim(->0+) Y(x) = +∞ 8, Первая производная. 6. Локальные экстремумы. Y'(x) = 0, x1 = - 3/2, x2 = 3/2 Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12. 7. Участки монотонности функции. Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2] 8. Вторая производная.
Корней нет. Точек перегиба (на графике) - нет. 9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
а1- авиакомпания 1
а2-авиакомпания 2
Пусть из некоторого города A нельзя попасть в некоторый город B по а1. Рассмотрим множество M всех городов, в которые можно попасть из города A по а1. Множество городов, не входящих в M, обозначим N. Множество N непусто, поскольку в нём содержится город B. Ясно, что из городов множества M нельзя попасть в города множества N по а1.
Докажем, что из каждого города в любой другой можно попасть по а2.
Если один из городов принадлежит M, а другой – множеству N, то между ними есть прямая авиалиния а2.
Пусть два города принадлежат M. Тогда из первого города можно попасть по а2 в некоторый город множества N, а оттуда (также по а2) – во второй город.
Аналогично рассматривается случай, когда оба города принадлежат N.
ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
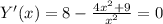
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении