Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a. После первой выплаты сумма долга составит: S1 = Sb − X. После второй выплаты сумма долга составит: S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X. После третьей выплаты сумма оставшегося долга равна: S3 = Sb³ - (1-b+b²)X = Sb³ - · X После четвертой выплаты сумма оставшегося долга равна: S4 = - (1 + b +b² + b³)X = - · X По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому - · X = 0. Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается: X = рублей
Пусть х - первое число, у - второе число. х/2 - половина первого числа. у/2 - половина второго числа. х/4 - четверть первого числа. у/3 - треть второго числа.
Умножим обе части первого уравнения на 6, И обе части второго уравнения на 4, чтобы избавиться от знаменателей: 6•х/2 = 6•4 + 6•у/3 4•у/2 = 4•18 + 4•х/4
3х = 24 + 2у или 2у = 3х -24 2у = 72 + х
Поскольку о обоих случаях равнениях равны левые части, то равны и правые. 3х-24 = 72+ х 3х-х = 72+24 2х = 96 х = 96:2 х = 48
Подставим значение х в уравнение 2у = 72 + х 2у = 72+48 2у = 120 у = 120:2 у = 60
ответ: 48 - первое число; 60 - второе число.
Проверка: 1) 48:2=24 - половина первого числа. 2) 60:3=20 - треть второго числа. 3) 24-20=4
Или
1) 60:2=30 - половина второго числа. 2) 48:4=12 - четверть первого числа. 3) 30-12=18
Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.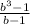 · X
· X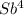 - (1 + b +b² + b³)X =
- (1 + b +b² + b³)X = 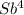 -
- 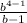 · X
· X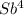 -
- 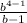 · X = 0.
· X = 0.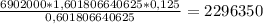 рублей
рублей
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -
После четвертой выплаты сумма оставшегося долга равна:
S4 =
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X =
х/2 - половина первого числа.
у/2 - половина второго числа.
х/4 - четверть первого числа.
у/3 - треть второго числа.
Составим два уравнения:
х/2 = 4+ у/3
у/2 = 18 + х/4
Умножим обе части первого уравнения на 6,
И обе части второго уравнения на 4, чтобы избавиться от знаменателей:
6•х/2 = 6•4 + 6•у/3
4•у/2 = 4•18 + 4•х/4
3х = 24 + 2у или 2у = 3х -24
2у = 72 + х
Поскольку о обоих случаях равнениях равны левые части, то равны и правые.
3х-24 = 72+ х
3х-х = 72+24
2х = 96
х = 96:2
х = 48
Подставим значение х в уравнение
2у = 72 + х
2у = 72+48
2у = 120
у = 120:2
у = 60
ответ: 48 - первое число; 60 - второе число.
Проверка:
1) 48:2=24 - половина первого числа.
2) 60:3=20 - треть второго числа.
3) 24-20=4
Или
1) 60:2=30 - половина второго числа.
2) 48:4=12 - четверть первого числа.
3) 30-12=18