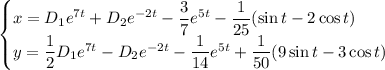Нам неизвестно первое слагаемое (х) , чтобы найти его из суммы (13/14 ) вычитаем первое слагаемое (3/14).
3/14+х= 13/14
х=13/14-3/14
х=10/14
3/14+10/14=13/14
13/14=13/14
Второе уравнение усложненное состоит из 2-х действии. 2 действие в скобке в левой части уравнения с неизвестным (у-3/8) оставляем . Сначала из уменьшаемого вычитаем разность . Теперь выполняем 2 действие (скобку) находим неизвестное У( уменьшаемое) , складываем (3,8) и (3/8). Проверка.
Предположим, что и не константы, а некоторые функции и .
Найдем первую производную:
Пусть . Тогда:
Найдем вторую производную:
Подставим значения функции и производных в уравнение относительно х:
Добавим к полученному уравнению условие, заданное на этапе нахождения первое производной:
Из первого уравнения выразим :
Подставим во второе уравнение:
Найдем :
Необходимо проинтегрировать выражения для и . Для этого предварительно вычислим следующие циклические интегралы, пользуясь формулой интегрирования по частям:
а) х= 10/14
б) у= 6/8
Пошаговое объяснение:
Нам неизвестно первое слагаемое (х) , чтобы найти его из суммы (13/14 ) вычитаем первое слагаемое (3/14).
3/14+х= 13/14
х=13/14-3/14
х=10/14
3/14+10/14=13/14
13/14=13/14
Второе уравнение усложненное состоит из 2-х действии. 2 действие в скобке в левой части уравнения с неизвестным (у-3/8) оставляем . Сначала из уменьшаемого вычитаем разность . Теперь выполняем 2 действие (скобку) находим неизвестное У( уменьшаемое) , складываем (3,8) и (3/8). Проверка.
5/8-(у-3/8)=2/8
у-3/8=5/8-2/8
у-3/8=3/8
у= 3/8+3/8
у= 6/8
5/8-(6/8-3/8)=2/8
2/8=2/8
Полное решение в прикрепленном файле, здесь некоторые подробные расчеты пропущены, так как слишком длинное решение не хочет добавляться.
Продифференцируем первое уравнение:
Подставим выражение для y' из второго уравнения:
От получившегося уравнения отнимем первое уравнение системы:
Решим однородное уравнение, соответствующее данному неоднородному:
Составим характеристическое уравнение:
Предположим, что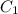 и
и 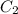 не константы, а некоторые функции
не константы, а некоторые функции 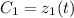 и
и 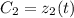 .
.
Найдем первую производную:
Пусть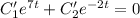 . Тогда:
. Тогда:
Найдем вторую производную:
Подставим значения функции и производных в уравнение относительно х:
Добавим к полученному уравнению условие, заданное на этапе нахождения первое производной:
Из первого уравнения выразим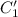 :
:
Подставим во второе уравнение:
Найдем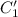 :
:
Необходимо проинтегрировать выражения для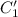 и
и 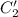 . Для этого предварительно вычислим следующие циклические интегралы, пользуясь формулой интегрирования по частям:
. Для этого предварительно вычислим следующие циклические интегралы, пользуясь формулой интегрирования по частям:
1)
2)
3)
4)
Интегрируем выражение для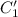 :
:
Интегрируем выражение для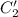 :
:
Подставляем выражения для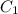 и
и 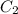 в решение:
в решение:
Найдем производную:
Из первого уравнения исходной системы выразим у:
Подставляем выражения для х и х':
ответ: