Всего возможны две ситуации: из конверта в конверт будет переложена простая задача или задача повышенной сложности.
Рассмотрим случай, когда будет переложена простая задача.
Найдем вероятность того, что из первого конверта во второй будет переложена простая задача. Для этого разделим число простых задач на общее количество задач в первом конверте:
После такого перекладывания во втором конверте окажется 5 простых задач и 8 задач повышенной сложности. Достать из такого конверта простую задачу можно с вероятностью:
Но такой конверт получается только с вероятностью . Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
Рассмотрим случай, когда будет переложена задача повышенной сложности.
Найдем вероятность того, что из первого конверта во второй будет переложена задача повышенной сложности:
После такого перекладывания во втором конверте окажется 4 простые задачи и 9 задач повышенной сложности. Достать из такого конверта простую задачу можно с вероятностью:
Но такой конверт получается только с вероятностью . Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
Поскольку события "переложить простую задачу" и "переложить задачу повышенной сложность" - несовместные, то общая вероятность достать простую задачу:
1. Запишите окончание предложения: 1) многочленом называют выражение, которое является ... суммой определенного количества одночленов; 2) многочлен, состоящий из двух членов, называют ...двучленом; 3) многочлен, состоящий из трёх членов, называют ...трехчленом; 4) многочленом стандартного вида называют многочлен, состоящий из ...одночленов, приведенных к стандартному виду; 5) степенью многочлена стандартного вида называют .... наибольшую степень одночлена, входящего в данный многочлен.
Чтобы понимать данные определения надо знать следующее: Одночлен - это алгебраическое выражение, которое состоит из произведения чисел, переменных, каждая из которых может входить в произведение в некоторой степени. Пример: . Есть константа(число) и переменные, содержащие степень. А например одночленом уже не будет. Далее, Одночлен называется представленным в стандартном виде, если он представлен в виде произведения числового множителя на первом месте и степеней различных переменных. т.е. например . Окей, дальше.
2. Какова степень многочлена: Определение степени мы уже знаем, так что легко решим. Очевидно, что тут это Точно также, тут тройка. Тут единица. Тут не очень понял условие, но в любом случае роли это не играет, ответ тут шесть(т.к. x во второй и y в четвертой в сумме дают 6). 3. Запишите многочлен в стандартном виде. 4. Запишите многочлен в стандартном виде. Тут я опять не уверен, что правильно понял степени. Но думаю, если я где-то ошибся, то вы справитесь самостоятельно, тут простые задачи. 5. Запишите выражение в виде: 1) суммы каких-либо двучленов; 2) разности каких-либо двучленов; 3) суммы одночлена и трёхчлена; 4) разности трёхчлена и одночлена. 6. Запишите в стандартном виде сумму многочленов и . 7. Запишите в стандартном виде разность многочленов и . 8. Запишите в стандартном виде разность многочленов и .
Всего возможны две ситуации: из конверта в конверт будет переложена простая задача или задача повышенной сложности.
Рассмотрим случай, когда будет переложена простая задача.
Найдем вероятность того, что из первого конверта во второй будет переложена простая задача. Для этого разделим число простых задач на общее количество задач в первом конверте:
После такого перекладывания во втором конверте окажется 5 простых задач и 8 задач повышенной сложности. Достать из такого конверта простую задачу можно с вероятностью:
Но такой конверт получается только с вероятностью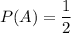 . Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
. Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
Рассмотрим случай, когда будет переложена задача повышенной сложности.
Найдем вероятность того, что из первого конверта во второй будет переложена задача повышенной сложности:
После такого перекладывания во втором конверте окажется 4 простые задачи и 9 задач повышенной сложности. Достать из такого конверта простую задачу можно с вероятностью:
Но такой конверт получается только с вероятностью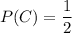 . Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
. Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
Поскольку события "переложить простую задачу" и "переложить задачу повышенной сложность" - несовместные, то общая вероятность достать простую задачу:
ответ: 9/26
1) многочленом называют выражение, которое является ... суммой определенного количества одночленов;
2) многочлен, состоящий из двух членов, называют ...двучленом;
3) многочлен, состоящий из трёх членов, называют ...трехчленом;
4) многочленом стандартного вида называют многочлен, состоящий из ...одночленов, приведенных к стандартному виду;
5) степенью многочлена стандартного вида называют .... наибольшую степень одночлена, входящего в данный многочлен.
Чтобы понимать данные определения надо знать следующее:
Одночлен - это алгебраическое выражение, которое состоит из произведения чисел, переменных, каждая из которых может входить в произведение в некоторой степени.
Пример:
Далее,
Одночлен называется представленным в стандартном виде, если он представлен в виде произведения числового множителя на первом месте и степеней различных переменных.
т.е. например
Окей, дальше.
2. Какова степень многочлена:
Определение степени мы уже знаем, так что легко решим.
Очевидно, что тут это
Точно также, тут тройка.
Тут единица.
Тут не очень понял условие, но в любом случае роли это не играет, ответ тут шесть(т.к. x во второй и y в четвертой в сумме дают 6).
3. Запишите многочлен в стандартном виде.
4. Запишите многочлен в стандартном виде.
Тут я опять не уверен, что правильно понял степени.
Но думаю, если я где-то ошибся, то вы справитесь самостоятельно, тут простые задачи.
5. Запишите выражение
1) суммы каких-либо двучленов;
2) разности каких-либо двучленов;
3) суммы одночлена и трёхчлена;
4) разности трёхчлена и одночлена.
6. Запишите в стандартном виде сумму многочленов
7. Запишите в стандартном виде разность многочленов
8. Запишите в стандартном виде разность многочленов