Пусть - точка касания.
Составим уравнение касательной:
Угловой коэффициент прямой, перпендикулярной x+3 будет равен -1 (-1/k).
То есть
Тогда уравнение касательной к f(x), перпендикулярной g(x) будет иметь вид
y=-x-4
Пусть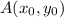 - точка касания.
- точка касания.
Составим уравнение касательной:
Угловой коэффициент прямой, перпендикулярной x+3 будет равен -1 (-1/k).
То есть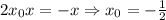
Тогда уравнение касательной к f(x), перпендикулярной g(x) будет иметь вид
y=-x-4