По условию, центр окружности принадлежит оси абсцисс, то есть лежит на оси Х, следовательно, координата по оси У равна нулю. Обозначим координаты центра окружности как (х',0).
Построим вектора из центра окружности О до точек А и В. Модуль вектора - корень из суммы квадратов его координат.
ОА={-4-x';1}, |OA|=
OB={8-x';5}, |OB|=
Модули векторов равны, так как точки лежат на окружности и, следовательно, равноудалены от центра на расстояние радиуса.
Пошаговое объяснение:
По условию, центр окружности принадлежит оси абсцисс, то есть лежит на оси Х, следовательно, координата по оси У равна нулю. Обозначим координаты центра окружности как (х',0).
Построим вектора из центра окружности О до точек А и В. Модуль вектора - корень из суммы квадратов его координат.
ОА={-4-x';1}, |OA|=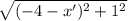
OB={8-x';5}, |OB|=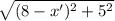
Модули векторов равны, так как точки лежат на окружности и, следовательно, равноудалены от центра на расстояние радиуса.
Значит, координаты центра окружности - (3,0).
Находим радиус окружности R=|OA|=|OB|=√(4+3)^2+1=√50.
Составляем уравнение окружности:
Примечание: жирным шрифтом выделены вектора.