Заметим, что каждый выписанный шифр запрещает 7*9=63 шифра (потому что существует ровно 9 чисел отличающихся от нашего в заданном разряде, а таких разрядов 7).
Заметим, что каждый невыписанный шифр похож не более чем на 7 выписанных (иначе существует два выписанных шифра, которые отличаются лишь в одном разряде, а это невозможно).
Теперь построим граф, в котором каждому шифру соответствует вершина, а между похожими шифрами проведено ребро. Тогда наш граф разобьется на две доли: выписанные шифры и запрещенные. Пусть выписано N1 шифров, запрещено N2. Тогда кол-во ребер в этом графе 63*N1<7*N2, т. е. 9N1≤N2, при этом N1+N2=10^7, получаем N1≤10^6.
Пример:
Докажем, что можно выписать 10^(n-1) n-циферных шифров.
База:
Решим задачу, для случая, когда кол-во разрядов равно 1. Тогда, очевидно, ответ - 1 (пример - любая цифра).
Переход:
У нас есть 10^(n-1) n-циферных шифров (попарно непохожих). Построим 10^n (n+1)-циферных шифров. Вначале припишем к каждому из начальных шифров слева цифру 0, получим 10^(n-1) (n+1)-циферных шифров. После этого припишем к каждому из начальных шифров цифру 1 и циклически переставим последнюю цифру (т.е. 0 превратится в 1, 2 в 3, 9 в 0), так мы получим еще 10^(n-1) шифров. Далее припишем к начальному набору слева 2, а последнюю цифру циклически переставим дважды (0 в 2, 1 в 3, 9 в 1). И так далее, приписываем цифру A слева, и делаем A циклических перестановок последней цифры.
Так мы получим 10 наборов по 10^(n-1) шифров, т.е. 10^n. Доказать, что все эти шифры не похожи друг на друга легко: внутри одного набора нет похожих, так как он сделан приписываением слева одной и той же цифры к двум уже не похожим числам и изменением последней цифра так, что разные цифры не могут стать одинаковыми. Два шифра из разных наборов, произошедшие от одного и того же шифра в начальном наборе отличаются в 2 цифрах - первой и последней. Два шифра из разных наборов произошедшие от разных шифров отличаются минимум в 2 цифрах - первой и какой-то еще не последней (она точно есть, т. к. в начальном наборе они были не похожи друг на друга).
1 000 000 (один миллион)
Пошаговое объяснение:
Оценка:
Заметим, что каждый выписанный шифр запрещает 7*9=63 шифра (потому что существует ровно 9 чисел отличающихся от нашего в заданном разряде, а таких разрядов 7).
Заметим, что каждый невыписанный шифр похож не более чем на 7 выписанных (иначе существует два выписанных шифра, которые отличаются лишь в одном разряде, а это невозможно).
Теперь построим граф, в котором каждому шифру соответствует вершина, а между похожими шифрами проведено ребро. Тогда наш граф разобьется на две доли: выписанные шифры и запрещенные. Пусть выписано N1 шифров, запрещено N2. Тогда кол-во ребер в этом графе 63*N1<7*N2, т. е. 9N1≤N2, при этом N1+N2=10^7, получаем N1≤10^6.
Пример:
Докажем, что можно выписать 10^(n-1) n-циферных шифров.
База:
Решим задачу, для случая, когда кол-во разрядов равно 1. Тогда, очевидно, ответ - 1 (пример - любая цифра).
Переход:
У нас есть 10^(n-1) n-циферных шифров (попарно непохожих). Построим 10^n (n+1)-циферных шифров. Вначале припишем к каждому из начальных шифров слева цифру 0, получим 10^(n-1) (n+1)-циферных шифров. После этого припишем к каждому из начальных шифров цифру 1 и циклически переставим последнюю цифру (т.е. 0 превратится в 1, 2 в 3, 9 в 0), так мы получим еще 10^(n-1) шифров. Далее припишем к начальному набору слева 2, а последнюю цифру циклически переставим дважды (0 в 2, 1 в 3, 9 в 1). И так далее, приписываем цифру A слева, и делаем A циклических перестановок последней цифры.
Так мы получим 10 наборов по 10^(n-1) шифров, т.е. 10^n. Доказать, что все эти шифры не похожи друг на друга легко: внутри одного набора нет похожих, так как он сделан приписываением слева одной и той же цифры к двум уже не похожим числам и изменением последней цифра так, что разные цифры не могут стать одинаковыми. Два шифра из разных наборов, произошедшие от одного и того же шифра в начальном наборе отличаются в 2 цифрах - первой и последней. Два шифра из разных наборов произошедшие от разных шифров отличаются минимум в 2 цифрах - первой и какой-то еще не последней (она точно есть, т. к. в начальном наборе они были не похожи друг на друга).
Функциональный ряд имеет вид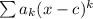
. Приведем наш ряд к такому виду.
Ряд содержит лишь четные степени (x+3), а значит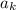
при нечетных 
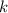можно взять равными 0. Т.е.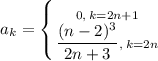 
Последовательность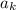
не имеет предела при 
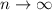, а значит необходимо использовать формулу Коши-Адамара.
Заметим, что последовательность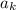
можно разбить на две подпоследовательности с конечными пределами, выделив нулевую подпоследовательность.
Тогда![\overline{lim}_{k\to \infty} \sqrt[k]{a_k}=\left [ MAX:\left \{ {{lim_{n\to \infty}\sqrt[2n+1]{0}=0} \atop {lim_{n\to \infty}\sqrt[2n]{\dfrac{(n-2)^3}{2n+3}}=1}} \right. \right ]=1=R=\dfrac{1}{\overline{lim}_{k\to \infty} \sqrt[k]{a_k}}=1](/tpl/images/1046/9024/56884.png)
Значит при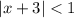
ряд сходится.
Исследуем сходимость на концах.
Если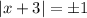
, получаем ряд 
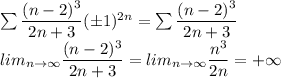- необходимое условие сходимости не выполнено, значит ряд расходится.
ответ: